機械と学習する

統計解析、機械学習について学習したことをまとめていきます

【統計検定準一級】統計学実践ワークブックの問題をゆるゆると解く#21

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズ
  • 第20回は9章「区間推定」から1問

【目次】

はじめに

本シリーズでは、いろいろあってリハビリも兼ねて統計学実践ワークブックの問題を解いていきます。 統計検定を受けるかどうかは置いておいて。

今回は9章「区間推定」から1問。

なお、問題の全文などは著作権の問題があるかと思って掲載してないです。わかりにくくてすまんですが、自分用なので。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

問9.1

問題

内閣支持率の世論調査を実施し、1,240人から回答があった。この回答を集計すると支持率は43%であった。（本当の調査かは知らないです）

f:id:hippy-hikky:20210526162753p:plain

(1) 回答者が母集団からの無作為抽出であると仮定したとき、95%信頼区間を求めよ

確率pで支持、(1-p)で不支持とすると、43%という集計結果は二項分布に従うことになります。

二項分布はベルヌーイ分布に従う確率変数の和となるので、中心極限定理からこれは正規分布で近似できることがわかります。

すると、二項分布の期待値と分散から、標準正規分布に従うz-scoreを導出できます。

f:id:hippy-hikky:20210526163117p:plain

このz-scoreが95%信頼区間の標準正規分布での下限と上限にかかる値を求めることで、信頼区間がもとまります。

f:id:hippy-hikky:20210526163534p:plain

この辺りの証明は、参考文献2を参考にしました。

(2) 支持率が40%前後と仮定したとき、95%信頼区間が2%となるために必要なサンプルサイズを求めよ

信頼区間の範囲から、幅は以下の式の通りとなります。


\begin{align}
 2 \cdot 1.96 \sqrt{\hat{p}(1-\hat{p})/n}
\end{align}

ここで、1.96は95%信頼区間なので1.96です。標準正規分布での2.5%, 97.5%の位置ですね。

f:id:hippy-hikky:20210526163646p:plain

【トップに戻る】

参考資料

【トップに戻る】

【統計検定準一級】統計学実践ワークブックの問題をゆるゆると解く#20

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズ
  • 第19回は8章「統計的推定の基礎」から1問（の半分）
    • 8章も厳しかった

【目次】

はじめに

本シリーズでは、いろいろあってリハビリも兼ねて統計学実践ワークブックの問題を解いていきます。 統計検定を受けるかどうかは置いておいて。

今回は8章「統計的推定の基礎」から1問。

なお、問題の全文などは著作権の問題があるかと思って掲載してないです。わかりにくくてすまんですが、自分用なので。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

問8.3

今回は、前回の続きです。問8.3長い。

問題

コイン工場で作られた5枚のコインについて。半径は以下の通り。


\begin{align}
 X = [ 8.4, 9.0, 8.2, 10.4, 9.2 ]
\end{align}

(4) ジャックナイフ推定量を用いてコインの面積のバイアス補正推定値を求めよ

(3)と同様に、T_1 = \bar{X}^2についてバイアスを補正した推定量を求めます。

バイアスの補正には「ジャックナイフ法」という手法を用いますが、この手法の証明等については追っておらず、テキストに記載の通りに実行しました。

f:id:hippy-hikky:20210525165452p:plain

このような標本を分割してバイアスを補正するなど推定値の精度を向上させる手法を「リサンプリング法」と呼ぶらしいです。手法としては手軽なので、何かで実用してみたいですね。

(5) デルタ法を用いてT1の漸近正規性を示せ

デルタ法というのは、7章で出てきたもので、f(\bar{X})の分布収束先を求める方法ということです（これも証明は追えていないです）。

ここでは、f(\bar{X})=\bar{X}^2なので、以下のメモの通りに漸近分散を求めることができます。

f:id:hippy-hikky:20210525170221p:plain

【トップに戻る】

参考資料

【トップに戻る】

【統計検定準一級】統計学実践ワークブックの問題をゆるゆると解く#19

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズ
  • 第19回は8章「統計的推定の基礎」から1問（の半分）

【目次】

はじめに

本シリーズでは、いろいろあってリハビリも兼ねて統計学実践ワークブックの問題を解いていきます。 統計検定を受けるかどうかは置いておいて。

今回は8章「統計的推定の基礎」から1問。

なお、問題の全文などは著作権の問題があるかと思って掲載してないです。わかりにくくてすまんですが、自分用なので。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

問8.3

問題

コイン工場で作られた5枚のコインについて。半径は以下の通り。


\begin{align}
 X = [ 8.4, 9.0, 8.2, 10.4, 9.2 ]
\end{align}

(1) \mu^2の二つの推定量についてバイアスを求めよ

二つの推定量については以下のメモを参照してください（見難くてすまんです。テキストを入手してください）。

バイアスは推定量の期待値から真値を引いたものなので、まずは推定量の期待値を求めます。今回の二つの推定量は、分散の式を利用して以下のメモのように導出できます。

推定量の期待値が導出できれば、あとは真値を引くだけ。

f:id:hippy-hikky:20210524232420p:plain

(2) コインの面積\pi r^2の推定値を各コインの面積の平均とすることの問題点

各コインの面積の平均は(1)のT2の推定量のπ倍の値になります。

そのため、(1)で求めたバイアスから、この推定値にはデータ数によらないバイアスが入ってしまいます。（つまり、不偏性がない）

f:id:hippy-hikky:20210524232835p:plain

(3) バイアスを補正した推定量を用いて、コインの面積のバイアス補正推定値を求めよ

(1)のT1のを以下のように補正するとのことです。


\begin{align}
 \tilde{T_1} = \bar{X}^2 - b_1(\bar{X}, U)
\end{align}

ここで、Uは不偏分散です。

T_1 = \bar{X}^2なので面積の推定値は\pi \tilde{T}_1となります。これを愚直に計算すると以下のメモのようになります。

f:id:hippy-hikky:20210524233158p:plain

【トップに戻る】

参考資料

【トップに戻る】

【統計検定準一級】統計学実践ワークブックの問題をゆるゆると解く#18

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズ
  • 第18回は8章「統計的推定の基礎」から1問

【目次】

はじめに

本シリーズでは、いろいろあってリハビリも兼ねて統計学実践ワークブックの問題を解いていきます。 統計検定を受けるかどうかは置いておいて。

今回は8章「統計的推定の基礎」から1問。

なお、問題の全文などは著作権の問題があるかと思って掲載してないです。わかりにくくてすまんですが、自分用なので。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

問8.2

問題

ポアソン分布に従って独立同一で取得されたn個の標本について。

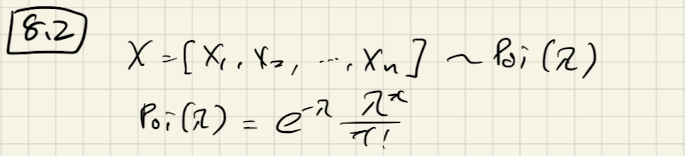
f:id:hippy-hikky:20210520173221p:plain

(1) パラメータ\lambdaの最尤推定量を求めよ

最尤推定量ということで、対数尤度関数の微分を求めれば良いです。

f:id:hippy-hikky:20210520173628p:plain

(2) \lambdaに関するフィッシャー情報量を求めよ

フィッシャー情報量はn個のデータについて以下の式で定義されています。（こちらの記事、参考文献3を参照）


\begin{align}
 I_n(\theta) = E[ \left\{ \frac{d}{d\theta}\log f_n(\mathbf{X} | \theta) \right\}^2 ]
\end{align}

対数尤度の微分の２乗の期待値です。

フィッシャー情報量I_n(\theta)の性質として、I_n(\theta)は標本一つの情報量のn倍という性質があります（以下のメモ）。また二乗の期待値の形を二階微分を使って表現することができます（以下のメモ）。これらの詳細は参考文献3などに詳しく書かれています。

これらを利用して、フィッシャー情報量I_n(\theta)は以下のメモの様に導出できます。

f:id:hippy-hikky:20210520174944p:plain

(3) \lambdaの最尤推定量が有効推定量であることを示せ

有効推定量とは、推定量の分散がフィッシャー情報量の逆数に等しくなることです（クラーメル・ラオの不等式の下限、こちらの記事、参考文献3）。ということで、最尤推定量\hat{\lambda}の分散を求めます。

f:id:hippy-hikky:20210520175448p:plain

ということで、有効推定量であることがわかりました。

(4) \lambdaの最尤推定量の漸近正規性、漸近有効性を示せ

最尤推定量\hat{\lambda}は標本平均です。標本平均は中心極限定理から漸近的に正規分布\mathcal{N}(\mu, \frac{\sigma^2}{n})に収束します（参考文献2, 参考文献3）。なので、漸近正規性が言えます。

漸近分散がフィッシャー情報量の逆数になることもそのまま出てきていますので、漸近有効であることもわかりました。

f:id:hippy-hikky:20210520175531p:plain

【トップに戻る】

参考資料

【トップに戻る】

【統計検定準一級】統計学実践ワークブックの問題をゆるゆると解く#17

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズ
  • 第17回は8章「統計的推定の基礎」から1問（#16の続き）

【目次】

はじめに

本シリーズでは、いろいろあってリハビリも兼ねて統計学実践ワークブックの問題を解いていきます。 統計検定を受けるかどうかは置いておいて。

今回は8章「統計的推定の基礎」から1問。8章はいきなり厳しくて、参考書を2冊追加してます（会社の経費で買った）。

なお、問題の全文などは著作権の問題があるかと思って掲載してないです。わかりにくくてすまんですが、自分用なので。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

問8.1

今回は、前回この問題については挑戦したのですが、(5)がよくわからなかったので再度やり直しています。

問題

正規分布\mathcal{N}(\mu, \sigma^2)からi.i.dで得た標本X=\{X_1, \cdots, X_n \}について

(5) 標本分散は分散\sigma^2の一致推定量であるが、漸近有効推定量ではないか？

まず、一致推定量であるかを確認します。一致推定量の定義から、推定量の分散とバイアスがn \rightarrow \inftyの極限で共に0になることが条件となります。これらを確認して一致性を持つと言うことが確認できました。なお、標本分散の分散とバイアスはこちらも合わせて参照ください。

「漸近有効性」については、調べたのですがまだよくわかっていません。正規分布の最尤推定量は漸近有効という記載はいくつかの書籍で確認したのですが、証明を追えていません。。。

f:id:hippy-hikky:20210517185350p:plain

【トップに戻る】

参考資料

【トップに戻る】

【統計検定準一級】第8章 統計的推定の基礎 #4【番外編】

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズの番外編
  • 8章「統計的推定の基礎」の内容をまとめます
  • 今回は推定量を評価する基準として、サンプルサイズが大きいときの漸近的な性質を議論します
    • 正直理解できてないです。折を見て再度挑戦しよう
  • おまけとして、不偏分散の導出も載せています

【目次】

はじめに

「統計学実践ワークブック(参考資料1)」の問題を解いていくシリーズをやっていく中で、8章「統計的推定の基礎」の内容をさっぱり理解していないことがわかったので、改めて整理しています。

参考にした資料は参考文献に列挙しています。中でも主に文献4を参考にしています。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

8章の流れ

統計の目的の一つとして、「未知パラメータの推定」という問題があり、この章ではその中でも「点推定」について扱っています*1。「区間推定」については9章で扱われています。

  • 情報の集約
    • 推論を行うにあたって、生データを全て保存するのではなく、情報を集約できればうれしい（メモリ的に）
    • → 「十分統計量」
  • 推定法
    • パラメータの点推定を行うためにはいくつか方法がある
    • → モーメント法
    • → 最尤推定
  • 推定量の評価、推定量の性質
    • 推定法は複数の方法がある。推定量は、真のパラメータ\theta *2の周辺に集中して欲しい。そこでその期待を満たすかをいくつかの指標で評価する。
    • → 不偏性
      • 推定量に偏り（バイアス）がない推定量が望ましい
      • → クラメール・ラオの不等式 : 不偏推定量の分散の下限を評価
      • → 有効推定量 : クラメール・ラオの不等式を満たす不偏推定量
    • → 漸近的性質
      • 標本サイズを大きくしたと仮定した場合の漸近的な評価基準についての議論
      • → 一致性 : 推定量が真のパラメータ\thetaに確率収束すること
      • → 漸近有効性 : 漸近的な分散が下限に達していること（クラメール・ラオの下限に対応）
      • → 一致性
      • → 漸近正規性

この流れに沿って、確認内容をまとめていこうと思います。

今回は推定量を評価する基準として、サンプルサイズが大きいときの漸近的な性質を議論します。

【トップに戻る】

推定量の性質

前々回は、パラメトリックなモデルにおけるパラメータの推論方法として、「モーメント法」と「最尤法」を扱いました。

パラメータの推論方法は他にも事後確率最大化法（MAP推定）などの方法がありますが、それらの推定量の性質を評価して、どのような推定量が好ましいのかを議論していきます。

漸近的性質

標本サイズnが大きい時の推定量の性質がわかれば、推定量が良いものか判断できます。

一致性(consistency)

推定量\hat{\theta}が一致性を持つとは、以下のようにnを大きくしていくと\hat{\theta}が真のパラメータ\thetaに確率収束することとあります。


\begin{align}
 \lim_{n \rightarrow \infty} P(|\hat{\theta}_n - \theta| \ge \epsilon ) = 0
\end{align}

以下の手書きメモにあるように、チェビシェフの不等式を使って導出できることがわかります。

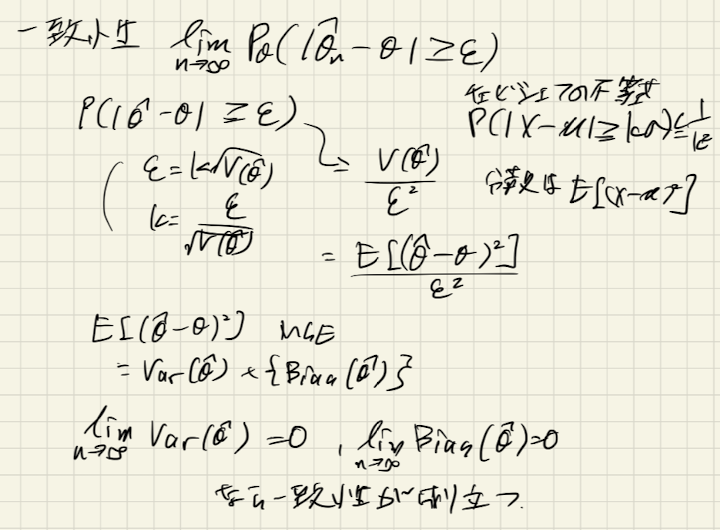
f:id:hippy-hikky:20210514172040p:plain

漸近有効性(asymptotic efficiency)

漸近有効性については、用語を整理するだけです（正直理解できてないところです）。

「有効推定量」というのは前回の議論で出てきましたが、分散がクラメール・ラオ下限な不偏分散でした。

「漸近」有効性ということで、漸近的な分散がクラメール・ラオの下限を示すというのが「漸近有効性」です。

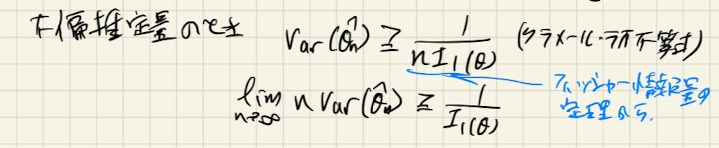
f:id:hippy-hikky:20210514173052p:plain

おまけ：分散の不偏性

これだけだと寂しいので、不偏分散の導出をおまけとしてまとめます。

分散といったら標本分散がよく使われていますが(最尤推定量ですし)、前回標本分散にはバイアスがあるということを述べました。そのため、不偏分散と比較していましたが、この不偏分散はなぜあの式なのかを証明してみます。

例によって手書きなので読みにくいと思いますが、やっていることはシンプルです。まず、標本分散の期待値を計算します。この期待値から、真の分散\sigma^2が期待値になるにはどうしたら良いかを考えます。

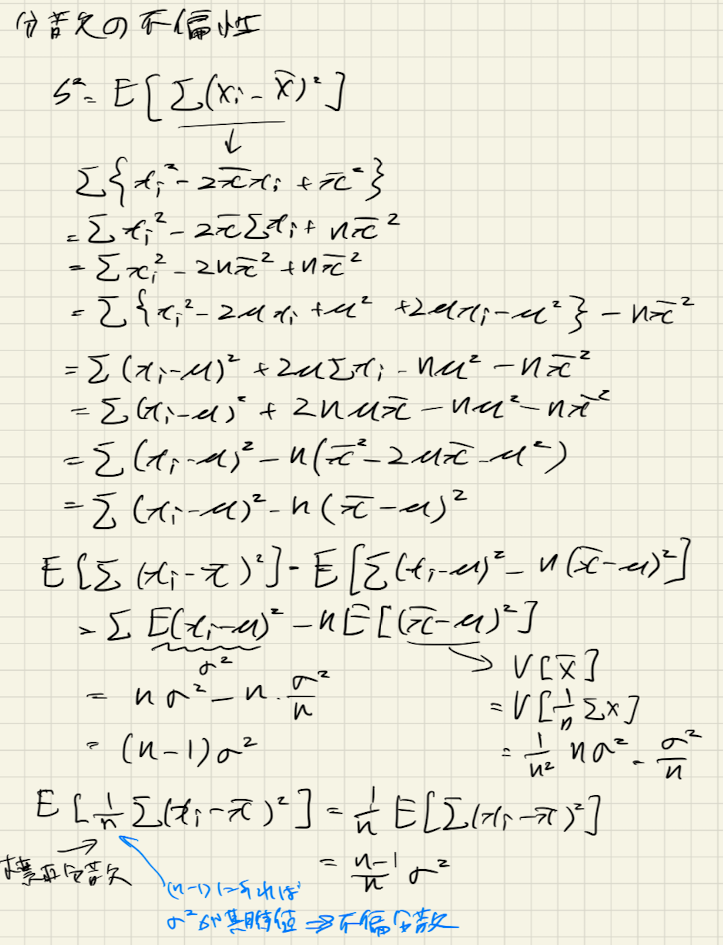
f:id:hippy-hikky:20210514173703p:plain

【トップに戻る】

参考資料

【トップに戻る】

*1:ここではパラメトリックなモデルを扱っています。ノンパラメトリックな方法については本書に記載があるのかは未確認です。

*2:真のパラメータってなんだ？という議論についてはここでは立ち入らないです。テキストの内容についてなるべく素直に読み解いていきます。

【統計検定準一級】第8章 統計的推定の基礎 #3【番外編】

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズの番外編
  • 8章「統計的推定の基礎」の内容をまとめます
  • 今回は推定量を評価する基準として「不偏性」という性質を扱います

【目次】

はじめに

「統計学実践ワークブック(参考資料1)」の問題を解いていくシリーズをやっていく中で、8章「統計的推定の基礎」の内容をさっぱり理解していないことがわかったので、改めて整理しています。

参考にした資料は参考文献に列挙しています。中でも主に文献4を参考にしています。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

8章の流れ

統計の目的の一つとして、「未知パラメータの推定」という問題があり、この章ではその中でも「点推定」について扱っています*1。「区間推定」については9章で扱われています。

  • 情報の集約
    • 推論を行うにあたって、生データを全て保存するのではなく、情報を集約できればうれしい（メモリ的に）
    • → 「十分統計量」
  • 推定法
    • パラメータの点推定を行うためにはいくつか方法がある
    • → モーメント法
    • → 最尤推定
  • 推定量の評価、推定量の性質
    • 推定法は複数の方法がある。推定量は、真のパラメータ\theta *2の周辺に集中して欲しい。そこでその期待を満たすかをいくつかの指標で評価する。
    • → 不偏性
      • 推定量に偏り（バイアス）がない推定量が望ましい
      • → クラメール・ラオの不等式 : 不偏推定量の分散の下限を評価
      • → 有効推定量 : クラメール・ラオの不等式を満たす不偏推定量
    • → 漸近的性質
      • 標本サイズを大きくしたと仮定した場合の漸近的な評価基準についての議論
      • → 一致性 : 推定量が真のパラメータ\thetaに確率収束すること
      • → 漸近有効性 : 漸近的な分散が下限に達していること（クラメール・ラオの下限に対応）
      • → 一致性
      • → 漸近正規性

この流れに沿って、確認内容をまとめていこうと思います。

今回は、推定量を評価する基準として「不偏性」という性質を扱います。

【トップに戻る】

推定量の性質

前回は、パラメトリックなモデルにおけるパラメータの推論方法として、「モーメント法」と「最尤法」を扱いました。

パラメータの推論方法は他にも事後確率最大化法（MAP推定）などの方法がありますが、それらの推定量の性質を評価して、どのような推定量が好ましいのかを議論していきます。

不偏性

推定量\hat{\theta}は、データによって結果が変わるので確率変数です。確率変数なので、なんらかのばらつきを持っています。

この推定量\hat{\theta}が有していて欲しい性質として、真のパラメータ\thetaの周辺にばらついて欲しいということがあります*3。データから推定したいのは真のパラメータ\thetaであり、全然別の所に推定量のピークが立っていても全然嬉しくないですからね。

さらに、推定量\hat{\theta}が\thetaを中心にしていても大きくばらついていたらうれしくないです。

ということで、推定量\hat{\theta}の期待値と分散を評価するのが、推定量の評価基準として第一に挙げられます。以下の手書きメモのように、\hat{\theta}の期待値が\thetaと一致する推定量を「不偏推定量(unbiased estimator)」と定義されています。

また、\hat{\theta}の期待値とthetaの差を「バイアス(bias)」と呼びます。

f:id:hippy-hikky:20210513220549p:plain

平均二乗誤差(MLE; Mean Squared Error)

ということで、バイアスと分散が小さくなる推定量だとうれしいです。

バイアスと分散を合わせて評価する指標として平均二乗誤差(MLE; Mean Squared Error)があります。平均二乗誤差自体はよく使われる指標ですけど、バイアスと分散を1:1で評価する指標という意味があったんですね。

f:id:hippy-hikky:20210513221135p:plain

不偏分散と標本分散(最尤推移定量)を比較する

分散の推定量として、不偏分散[tex:V2]と標本分散[tex:S2]があります。とくに、標本分散は前回取り上げた最尤推定の結果として得られているもので、よく使われます。一方不偏分散は、上記の不偏性で触れたようにバイアスが0の推定量です*4。

どっちが好ましい推定量でしょうか？というのを確認してみます。参考文献[4]に記載の例題なので、詳しくはそちらを。

ここでは、サンプルは正規分布\mathcal{N}(\mu, \sigma^2)に従って独立に得られているとします。

まず、Qという量を定義しています。これは、カイ二乗分布に従う性質があることがわかっています*5。

f:id:hippy-hikky:20210513221916p:plain

カイ二乗分布に従う確率変数の期待値と分散の性質*6から、バイアス、分散が計算でき、これらを合わせてMSEを求めることができます。

f:id:hippy-hikky:20210513222639p:plain

実際に不偏分散と標本分散について、バイアス、分散、MSEを比較した結果、標本分散は分散とMSEが小さくなることがわかりました。

f:id:hippy-hikky:20210513222710p:plain

この結果から、標本分散の方が望ましいといって良いかは微妙なところです。推定量は真のパラメータとずれたところにピークが出ている可能性があるということなので。

分散はどこまで小さくできる？>クラーメル・ラオの不等式

不偏推定量はバイアスが0なので、分散が小さいほど良い推定量です。

この分散がどこまで小さくできるのか？という疑問がわきますが、この分散の下限は計算することができるようです。この下限をクラーメル・ラオの下限と呼んでいるようです。

この下限ですが、フィッシャー情報量の逆数で定義されるとのことです。フィッシャー情報量は以下のメモに記載のように、対数尤度の勾配の期待値となっています。勾配が鋭いほど分散が小さいということですし、データが多くなる程推定量の分散は小さくなっていきます。

f:id:hippy-hikky:20210513223359p:plain

正規母集団を例にしてクラーメル・ラオの下限を計算してみる

（これも詳しくは参考文献[4]を参照してください）

分散1として、平均パラメータμが未知の正規母集団に従う確率変数Xを考えます。 実際の計算は参考文献[4]に記載のフィッシャー情報量の3つの性質を使って容易に導出することができます(命題の証明は追ってない。。。)。

f:id:hippy-hikky:20210513224222p:plain

有効推定量とは？

参考文献[1]に書かれていますが、クラーメル・ラオの不等式の下限となる不偏推定量のことを「有効推定量（efficient estimator）」と呼ぶらしいです。

分散が最小の不偏推定量(=バイアスが0)なので、この推定量が最も良い推定量ということになります。

【トップに戻る】

参考資料

【トップに戻る】

*1:ここではパラメトリックなモデルを扱っています。ノンパラメトリックな方法については本書に記載があるのかは未確認です。

*2:真のパラメータってなんだ？という議論についてはここでは立ち入らないです。テキストの内容についてなるべく素直に読み解いていきます。

*3:「真のパラメータ」についてはここでは深入りしません。

*4:逆に言うと、標本分散は真のパラメータとズレがあり、特にデータが少ない時に顕著になる。

*5:ここでは証明はおっていません。詳しくは参考文献[4]で。

*6:これも詳しくは参考文献[4]で。