ベイズ線形回帰（解析解）の実装

【2020/07/09更新】

添付のnotebookに一部間違いがあったので修正しました。修正箇所は更新済みのnotebookのセル番号[19]。
- 予測分布の分散の計算で、分散(var_y)を足さなければいけないところを標準偏差(sqrt(var_y))を足してしまっていたので修正しました。
- 予測分布の可視化結果に違和感があったのがなくなりました。コメントありがとうございます。

【概要】

ベイズ推論について理解するために実装するシリーズの第２弾
今回は線形回帰のパラメータ推論（いわゆる学習）を確率推論するベイズ線形回帰を実装してみました

【目次】

はじめに
本記事の範囲
線形回帰
- 線形回帰のモデル
- 線形回帰の学習
ベイズ線形回帰
おわりに
おまけ
参考文献

はじめに

ベイズ推論についての書籍をいくつか読んでいて、なんとなく理解はできても具体的なイメージってつきにくくないですか？
ということで、実装して理解を深めたいと思います。

この記事では、線形回帰のパラメータ推論を確率推論するベイズ線形回帰について、概要をまとめ、実装してみます。よく使われる確率分布の可視化を行った前回の記事の続きです。

前回の記事はこちら↓

learning-with-machine.hatenablog.com

参考にした書籍は、「ベイズ深層学習」です。

ベイズ深層学習 (機械学習プロフェッショナルシリーズ)

作者:須山敦志
発売日: 2019/08/08
メディア: 単行本（ソフトカバー）

間違いなどあったら指摘していただけると助かります。

【トップに戻る】

本記事の範囲

本記事では、ベイズ深層学習の3章の内容を実装していきます。前回も書きましたが、よく出てくる確率分布の紹介とベイズ線形回帰までを一つの記事で書くつもりだったのですが、確率分布の章が思いの外長くなってしまったため、記事を分割することにしました。本記事は後編となります。

後編では、ベイズ線形回帰を扱います。

実装については、以下のjupyter notebookに載っています。上記の理由から、前回載せたnotebookと同じものです。

gist47ca094d0ee45af92eed3a8b9b3c09ec

【トップに戻る】

線形回帰

ベイズ線形回帰に入る前に、線形回帰について簡単に復習しておきます。線形回帰について詳しくは、ベイズ深層学習の2章やPRML(上)の第3章などを参照してください。

線形回帰のモデル

線形回帰とは、入力変数 $\mathbf{x} \in \mathbb{R}^D$ と重みベクトル $\mathbf{w} \in \mathbb{R}^D$ の線型結合で実数出力 $y \in \mathbb{R}$ を予測するためのモデルです。

${ \displaystyle y = \mathbf{w}^T \mathbf{x} + \epsilon }$

ここで、 $\epsilon$ はノイズ成分です。

入力変数 $\mathbf{x}$ が1次元の場合を特に「単回帰」、2次元以上の場合を「重回帰」と呼ぶことが多いと思います。また、入力変数にM個の何らかの関数( $\mathbf{\phi(x)} = \left( \phi_1(x), \cdots, \phi_M(x) \right)^{T}$ )をかけてM次元の入力変数にして、M次元の重みベクトル $\mathbf{w} \in \mathbb{R}^M$ との線型結合としたモデル(以下の式)も線形回帰と呼ばれます。

${ \displaystyle y = \mathbf{w}^T \mathbf{\phi}(x) + \epsilon }$

$\mathbf{\phi(x)}$ の操作は「特徴抽出」と呼ばれることが多いです。

線形回帰の学習

線形回帰の学習には、まず、入力と出力のペア $(\mathbf{x}, y)$ をデータセットとして多数用意します。このデータセット( $\mathcal{D}$ )に対して最も当てはまる関数を推定することが「学習」です。線形回帰モデルでは、入力変数と重みベクトルの内積を関数の形としているため、重みベクトル $\mathbf{w}$ をデータから推定することが学習となります。

実際の学習方法には、最小二乗法と呼ばれる、以下の誤差関数 $E(\mathbf{w})$ を最小化する $\mathbf{w}_{LS}$ を算出する方法がよく用いられます。

${ \displaystyle E(\mathbf{w}) = \frac{1}{2} \sum^{N}_{n=1} \left\{ y_n - \mathbf{w}^T\mathbf{\phi}(x_n) \right\}^2 }$

また、最尤法という手法も同様によく用いられます。最尤法では、ノイズ成分がどのような分布かを仮定し、以下のように確率モデル化します。

${ \displaystyle y_n = \mathbf{w}^T \mathbf{\phi}(x) + \mathcal{N}(\epsilon | 0, \sigma^{2}) \\ \ \ \sim p(y_n | x_n, \theta) = \mathcal{N}( \mathbf{w}^{T} \mathbf{\phi}(x) , \sigma^{2}_y) }$

ここでは、ノイズ成分を $\epsilon \sim \mathcal{N}(0, \sigma^{2}_y)$ （ガウスノイズ）と仮定しました。そして、データの当てはまりを評価するための関数である尤度関数を設計します。

${ \displaystyle L(\theta | \mathbf{X}, \mathbf{Y}) = \prod^{N}_{n=1} p(y_n | x_n, \theta) }$

$\theta$ は調整可能なパラメータを表します。ここでは、重みベクトル $\mathbf{w}$ やノイズの分散 $\sigma^{2}$ です*1。

このように尤度関数を設計し、この尤度関数が最大となるパラメータ $\theta$ を求めるのが最尤法です。最尤法の計算は、上式のままでは計算がしにくいため、対数をとった対数尤度を最大化することを考えます。

計算は省略しますが、ノイズ成分を正規分布と仮定したモデルでは、最小二乗法と最尤法は一致します。

余談ですが、最尤推定についてどの書籍を引用するべきかピンと来ず。オススメの書籍などあれば紹介いただけると助かります。私の知ってる範囲では、最尤法がメインではないですが、「ガウス過程と機械学習」は丁寧に説明がある印象でした。また、ちょっと古い本ですが、「自然科学の統計学」にも詳しく書かれていたと思います。

【トップに戻る】

ベイズ線形回帰

続いて、ベイズ線形回帰です。
基本的なモデルは上記の最尤法で立てたモデルと同じですが、ベイズ線形回帰では、推定対象となるパラメータ*2に確率分布を仮定します。つまり、パラメータはある確率分布に従う確率変数であると考えます。

上記の線形回帰をベイズ化してみます。

予測したい出力 $y_n$ は、入力 $x_n$ と重みベクトル $\mathbf{w}$ に依存します。入力 $x_n$ は所与ですが、重みベクトル $\mathbf{w}$ は未知であり、これを推定したいのでした。 $\mathbf{w}$ は未知の変数であり、これに確率分布を仮定します。

重みベクトル $\mathbf{w}$ が従う分布として、平均0で分散が $\sigma^{2}_{w}$ のガウス分布に従うと仮定します。なお、分散 $\sigma^{2}_{w}$ は固定のハイパーパラメータとします。すると、モデル全体の確率変数の同時確率は以下のようになります。

${ \displaystyle p(X, Y, \mathbf{w}) = p(Y | \mathbf{w}, X)p(\mathbf{w}) = p(\mathbf{w}) \prod^{N}_{n=1}p(y_n | \mathbf{w}, x_n) }$

ここで、 $X=\{x_1, x_2, \cdots, x_N\}, Y=\{y_1, y_2, \cdots, y_N\}$ です。

同時確率を立てられたなら、データ（XとYのペア）が与えられた元での重みベクトル $\mathbf{w}$ の事後確率 $p(\mathbf{w}|Y, X)$ を求めます。なお、出力yの従う分布は先に書いた最尤推定のモデルと同じものとし、分散 $\sigma^{2}_y$ は固定のハイパーパラメータとします。
事後確率は、 $p(\mathbf{w}|Y, X) \propto p(Y | \mathbf{w}, X)p(\mathbf{w})$ であり、これの対数をとって整理すると以下のガウス分布となります。詳しくは、ベイズ深層学習を参照してください。

${ \displaystyle p(\mathbf{w} | \mathbf{Y}, \mathbf{X}) = \mathcal{N}(\mathbf{w} | \hat{\boldsymbol{\mu}}, \hat{\mathbf{\Sigma}}) }$

${ \displaystyle \ \ \hat{\mathbf{\Sigma}}^{-1} = \sigma_{y}^{-2} \sum_{n=1}^{N} \phi\left(\mathbf{x}_{n}\right) \phi\left(\mathbf{x}_{n}\right)^{T}+\sigma_{w}^{-2} \mathbf{I} \\ \ \ \hat{\mu} = \hat{\Sigma} \sigma_{y}^{-2} \sum_{n=1}^{N} y_{n} \phi\left(\mathbf{x}_{n}\right) }$

今回は線形回帰モデルなので、共役な分布の関係を利用して事後確率を解析的に算出することができました。共役な関係の分布については、前回の記事が参考になるかもしれません。

回帰モデルを推定することができたなら、未知の入力 $x_*$ に対しての予測値を得たいです。ベイズ線形回帰では重みベクトルは上記のように事後確率分布として得られているため、未知の値の予測値も以下のように分布（予測分布）として得られます。計算の詳細は、ベイズ深層学習などを参照ください。

${ \displaystyle p\left(y_{*} | \mathbf{x}_{*}, \mathbf{Y}, \mathbf{X}\right) = \mathcal{N}\left(y_{*} | \mu_{*}\left(\mathbf{x}_{*}\right), \sigma_{*}^{2}\left(\mathbf{x}_{*}\right)\right) }$

${ \displaystyle \ \ \mu_{*}\left(\mathbf{x}_{*}\right) = \hat{\boldsymbol{\mu}}^{T} \boldsymbol{\phi}\left(\mathbf{x}_{*}\right) \\ \ \ \sigma_{*}^{2} \left(\mathbf{x}_{*}\right) = \sigma^{2} + \phi\left(\mathbf{x}_{*}\right)^{T} \hat{\mathbf{\Sigma}} \phi\left(\mathbf{x}_{*}\right) }$

では、以上の結果を実装して確認してみましょう。

モデルの構築

今回は入力 $x$ は1次元の実数値のケースを扱います。基底関数（特徴量関数）は多項式とします。つまり、多項式回帰を行います。

出力 $y$ 、重みベクトル $\mathbf{w}$ がそれぞれ従う分布を以下のように仮定します。

${ \displaystyle y \sim \mathcal{N}(y | \mathbf{w}\mathbf{\phi}(x), \sigma^2_y)\\ w \sim \mathcal{N}(\mathbf{w} | \mathbf{\mu}, \sigma^2_w \mathbf{I}) }$

このモデルに従って、関数をサンプルしてみました*3。

f:id:hippy-hikky:20191029140329p:plain — 事前分布からサンプルした３次関数の例．

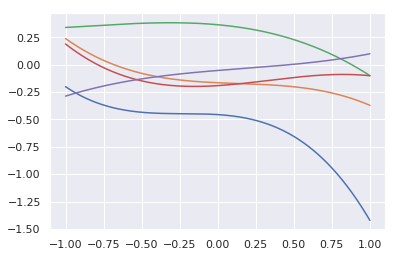
上記の図は３次関数を5本サンプルした結果です。まだデータを観測していないので、それぞれバラバラの関数ですが、こんな感じの関数が表現できるという雰囲気を感じられるのかなと思います。

実装のコードはnotebookのセル[13]です。

トイデータの作成

パラメータの推論をやってみるために、入力データを作成してみます。

今回は次の関数から10点のデータをサンプルしてみました。

${ \displaystyle y = \alpha * \sin(x * \omega) + \epsilon \\ \epsilon \sim \mathcal{N}(0, \sigma^2) }$

下図のオレンジ色の点がサンプルした点になります。

f:id:hippy-hikky:20191029141134p:plain — 真の関数とサンプルデータ．実線が真の関数（正弦波）を表し，オレンジ色の点が真の関数からサンプルした点を表す．

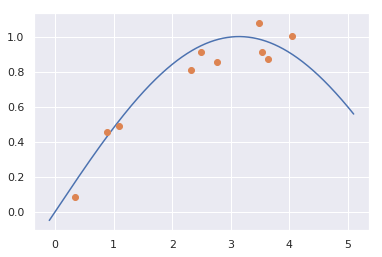
トイデータのサンプルについては、notebookのセル[14]に書いています。

ベイズ線形回帰の学習（重みwの事後分布）

上記のサンプルデータから、線形回帰モデルのパラメータ $\mathbf{w}$ を推定してみます。

先に書いた通り、事後分布は以下の式として解析的に求めることができたのでした。

${ \displaystyle p(\mathbf{w} | \mathbf{Y}, \mathbf{X}) = \mathcal{N}(\mathbf{w} | \hat{\boldsymbol{\mu}}, \hat{\mathbf{\Sigma}}) }$

この事後分布に従ってパラメータを推定します。推定は添付のnotebookのセル[15]に実装しています。

事後分布からwのサンプル

推定した事後分布から関数（重みベクトル $\mathbf{w}$ ）をサンプルしてみます。

f:id:hippy-hikky:20191031000541p:plain — 事後分布からパラメータwのサンプル．wを10個サンプルして関数を描いたもの．

先に描いた事前分布からサンプルした関数群と比較すると、今回サンプルした10本の関数は似たような関数ですね。たった10点のデータですが、データに基づいて事後分布を推定したことで、回帰式の範囲が狭まったことがわかります。

こちらを実装しているのは、notebookのセル[16, 17]です。

予測分布の算出

推定したパラメータの事後分布に基づいて、未知の入力データ( $x_*$ )に対する出力 $y_*$ の予測分布を算出してみます。

${ \displaystyle p\left(y_{*} | \mathbf{x}_{*}, \mathbf{Y}, \mathbf{X}\right) = \mathcal{N}\left(y_{*} | \mu_{*}\left(\mathbf{x}_{*}\right), \sigma_{*}^{2}\left(\mathbf{x}_{*}\right)\right) }$

解析解を使って予測分布を描いてみました。 (注. 2020/07/09更新)

f:id:hippy-hikky:20200709224510p:plain — 予測分布(左)．青線が予測分布の平均．グレーの領域が平均から±σの範囲．オレンジ線は真の関数を表す．右図は予測の標準偏差σの大きさをプロットしたもの．

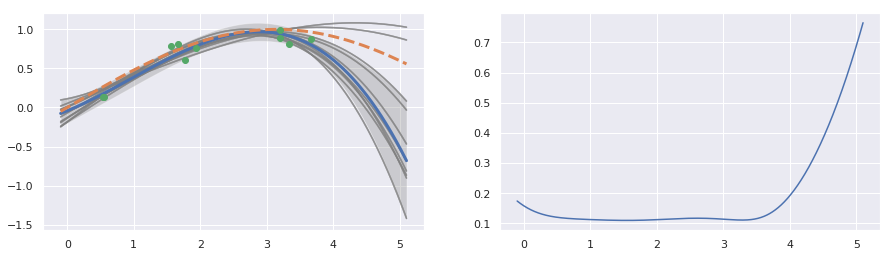
上の右図から、データが少ないところでばらつき（分散）が大きくなる傾向にあることがわかります。

予測分布の算出とプロットは、notebookのセル[18, 19]です。

【トップに戻る】

おわりに

ということで、ベイズ線形回帰の解析解を算出し、データから推定できた事後分布に基づいて関数を描いてみました。今回は３次関数を基底関数に選択したため、データが少なくても概ねバラツキの少ない関数を推定することができました。これが、もっと複雑な関数を推定したい場合にガウス基底などを使うと、予測分布のバラツキが大きくなるのだろうと想像します。

今回はこれで終わりですが、今後新たに実験をしたらその結果も紹介したいと思います。

【トップに戻る】