Juliaを使ってギブスサンプリングで線形回帰(多項式回帰)する
【概要】
【目次】
はじめに
良い良いとすごく評判のJulia言語を触ってみました。
ここでは、Juliaの練習として、線形回帰(多項式回帰)をベイズ的に推論する「ベイズ線形回帰モデル」の推論をやってみます。 ベイズ線形回帰の推論は、行列演算、制御構文(ループ)、描画あたりが全て含まれていて良い題材と思います。
また、私が普段使っているプログラミング言語であるPythonとの比較として、(厳密ではないですが)計算速度の定量的な比較と、使ってみた感想を定性的な比較として列挙してみます。
間違いなどあったら指摘していただけると助かります。
実験環境
実験環境はMac mini (Apple M1チップ)でJupyter labで書いています。環境構築について詳しくは私の書いた以下のQiita記事を見てください。
線形回帰モデル
線形回帰モデルは、入力ベクトルと重みベクトル
の線型結合で目的変数
を表現するモデルです。
当ブログでは、線形回帰モデルについては何度か扱っていますので、モデルの詳細については以下の記事などを合わせて参照していただけたらと思います。
learning-with-machine.hatenablog.com
では、今回扱うモデルを定義していきます。
システムモデル
今回は、システムノイズはないとして、以下の通り入力ベクトルと重みベクトル
の線型結合とします。
![]()
ここで、入力ベクトルは以下の通り、k次の冪乗を特徴量としています。
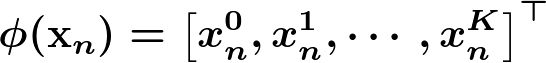
観測モデル
上記のシステムモデルに対して、観測時にはガウスノイズが乗ってくるとします。
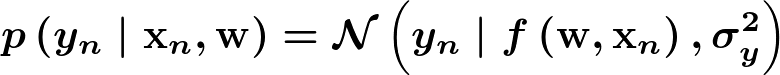
ここで、観測ノイズの分散は既知のパラメータとします。
重みベクトルの事前分布
重みベクトルの事前分布は、以下の通り各次元独立な多変量ガウス分布とします。
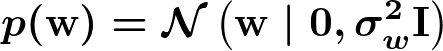
同時分布
ということで全体を結合して、今回推論するモデルは以下の通りです。
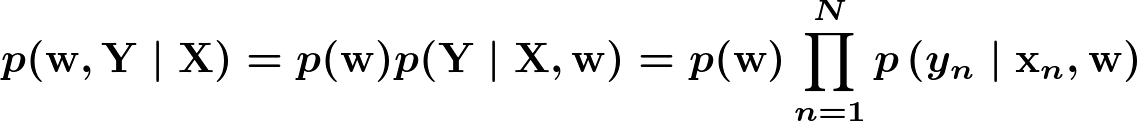
モデルの推論
線形回帰モデルは重みベクトルの事前分布にガウス分布を利用すれば解析的に解を導出できます。
ですが、プログラミングの練習として、ここではギブスサンプリングによる近似解も合わせて計算します。
解析解
複数の観測データを使って上記モデルを推論した結果としての重みベクトルの事後分布
は以下の記事にあるように導出できます。(以下の記事では手書きで導出過程を書いています。汚い手書きでごめんなさい)
learning-with-machine.hatenablog.com
近似解(Gibbs sampling)
MCMCアルゴリズム(ギブスサンプリング)を利用して近似解も推論してみます。
今回は、単変量ガウス分布からのサンプルは容易だが、多変量ガウス分布からのサンプルは難しいと仮定して、の各次元について独立にサンプルすることにします。
i次元の重みのサンプルを取得するにはi次元以外の重み
を固定とした条件付き分布を導出する必要がありますが、その導出については以下の記事に導出過程を掲載しています。(これも汚い手書きでごめんなさい)
learning-with-machine.hatenablog.com
実装
トイデータ
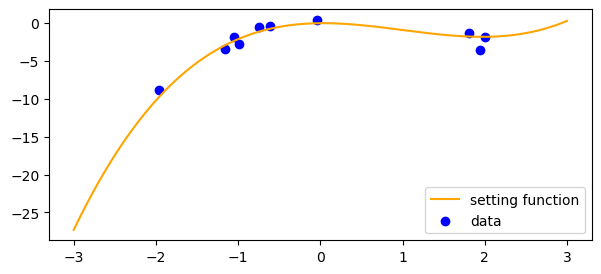
今回扱うトイデータは、3次の多項式に従う以下の関数(オレンジ線)からサンプルします。サンプルしたデータは青点で描画しています。
実装で詰まったところ
Distributions.jlのMvNormalを利用して多変量ガウス分布に従う乱数を生成するところで、解析的に算出した共分散行列を入力したら以下のエラーが出てしまいました。
ERROR: PosDefException: matrix is not Hermitian; Cholesky factorization failed.
ここの議論でSymmetric関数を通せば良いということは分かったのですが、Symmetric関数を通しても(通す前と)行列の各値は同じように見えますし。。。エルミート行列とか全然理解していないので、よく分からず対応したままです。
推論結果
推論に利用したコードは以下のリンクを参照してください。
Juliaでの実装 → gibbs_sampling_regression_julia.ipynb · GitHub
Pythonでの実装 → gibbs_sampling_regression_python.ipynb · GitHub
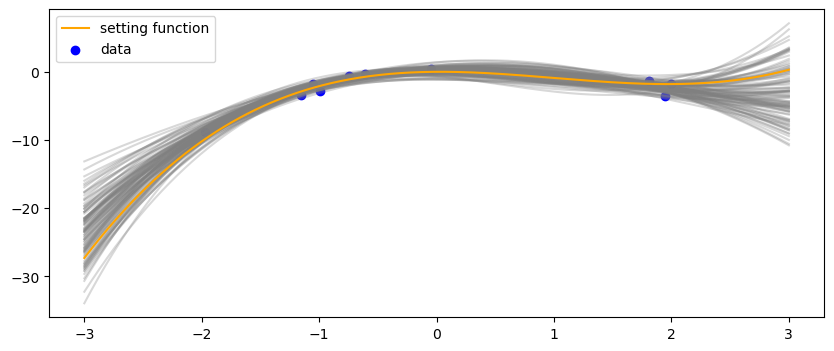
推論したの事後分布
に基づいて関数を100本サンプルして上記のトイデータのグラフに重ねた結果は以下の通りです。
まずは解析解
こちらは近似解
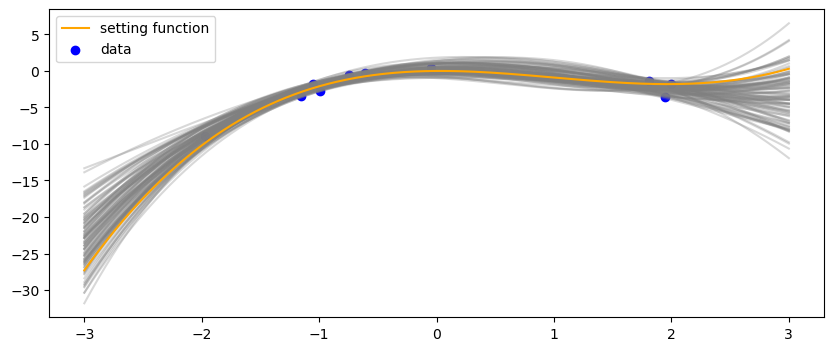
解析解と近似解は(当然ですが)同じような結果になってくれました。上記のリンク先のnotebooにはの分布も合わせて掲載しており、それを見ても同じような結果になっていることが分かります。
データが少ないところは、関数のバリエーションが広がっているということが分かります。なお、これは予測分布ではないので注意です。
Pythonとの比較
計算速度の比較。
| 解析解[sec] | ギブスサンプリング 10,000サンプル[sec] | |
|---|---|---|
| Python | 0.021 | 6.91 |
| Julia(コンパイル込み) | 6.27 | 2.10 |
| Julia(コンパイル無し) | 0.0003 | 0.40 |
「コンパイル込み」とは、Jupyterで最初に関数を実行した際の計算時間です。「コンパイル無し」とは、2度目に実行した結果です。(という理解であっているんでしょうか??)
訂正的な比較。
- Juliaはmatlabぽい
- 公式ページにも書いてある
- 行列演算が直接書けるので、数式を比較的そのまま書ける気がする
Pythonの方が仕事でも何年も使っているので当然すんなり書けるのですが、Juliaは数式に近い形でコードを書けるような気がするので、書きやすいかもなーという感じはしました。が、正直Juliaはまだよくわかってないです。
最適化の余地はまだまだあるのでしょうけど、ループが入るような計算は期待通りJuliaがだいぶ速そうです。これは仕事でもJuliaを推していった方が良いかも。
ただ、繰り返しが入らないような単発の処理についてだけ見ると、Pythonの方が処理は速く終わりました。コンパイルしてるからなんでしょうけど。ほんとに単発でしか実行しない処理なら別ですが、パラメータを変えて何度か試すような場合などJuliaで事前にコンパイルしておくと、この点も解消されるのかなと思いました。
おわりに
ということで、Juliaを使って線形回帰モデルを書いてみました。
最適化の余地はどちらもあると思いますが、同程度に雑に書いたJuliaコードとPythonコードの計算時間を比較すると、 forループを使うような処理の場合はコンパイル時間含めてもJuliaの方が速そうでした。ものに依るのでしょうけど。 速度以外にも、Juliaでは行列演算が素直に書けるの良さそうに感じました(matlabみたい)。

