機械と学習する

統計解析、機械学習について学習したことをまとめていきます

トップ > 統計モデリング > 系列データの統計モデリング　〜自己組織型状態空間モデルを利用した状態推定モデルのハイパーパラメータ推定〜

系列データの統計モデリング　〜自己組織型状態空間モデルを利用した状態推定モデルのハイパーパラメータ推定〜

統計モデリング 系列データ パーティクルフィルタ

【概要】

  • パーティクルフィルタを利用して系列データのモデリングと状態推定をやってみます
  • 今回は、固定点平滑化を応用した状態空間モデルのパラメータ推論である自己組織化状態空間モデルを試してみます

【目次】

はじめに

統計モデリングを行うにあたって、独立同分布(i.i.d; independent and identically distributed)を仮定することが多いと思います。

しかし、i.i.dを仮定できないケースはよくあります。時系列などの系列データが代表的です。また、i.i.dを仮定することが多い対象でも、計測対象や計測装置の経時的な変化（劣化）など本来的には系列を考慮しないといけない場面はあると思います。

系列データの解析について、主に「予測にいかす統計モデリングの基本」を参考に確認しましたので、数回に分けてまとめていこうと思います。なお、状態空間モデル(State Space Model)を使ったモデリングが対象です。私個人的には状態空間モデルでのモデリング経験はあるのですが、平滑化やパラメータ推論の理解が曖昧でしたので、このあたりの整理をメインに考えています。

第2回では状態空間モデルのパラメータを直接法を用いて推論しました。しかし、直接法ではちょっと複雑なモデルになると探索空間が広くなり、計算に非常に時間がかかってしまいます。

そこで今回は、固定点平滑化を応用したパラメータ推論を行います。状態推定と同時にパラメータの事後分布を推論します。

間違いや勘違いなど、なにかありましたら指摘いただけるとすごく助かります。

No. リンク
第1回 系列データの統計モデリング 〜パーティクルフィルタによる状態推定〜 - 機械と学習する
第2回 系列データの統計モデリング 〜ハイパーパラメータの推定〜 - 機械と学習する
第3回 これ
第4回 系列データの統計モデリング 〜カルマンフィルタ の導出と実装〜 - 機械と学習する

【トップに戻る】

平滑化

第1回で予測分布とフィルタ分布のについてのパーティクルフィルタを利用した推論を扱いました。

本稿では平滑化分布について扱います。

平滑化

第1回で書きましたが、時間の取り方で事後分布は以下の3つの分布が考えられます。


\begin{align}
   p(x_t | y_{1:t-1}) \cdots (1) \\
   p(x_t | y_{1:t}) \cdots (2) \\
   p(x_t | y_{1:T}) \cdots (3)
\end{align}

(3)が今回注目する平滑化分布です。これを周辺化を利用して展開してみます。


\begin{align}
  p(x_t | y_{1:T}) &= \int p(x_t, x_{t+1} | y_{1:T}) dx_{t+1} \\
    &= \int p(x_t | x_{t+1}, y_{1:t}) p(x_{t+1} | y_{1:T}) dx_{t+1} \\
    &= p(x_t | y_{1:t}) \int \frac{p(x_{t+1} | x_t)}{p(x_{t+1} | y_{1:t})} p(x_{t+1 | y_{1:T}}) dx_{t+1}
\end{align}

1行目から2行目は乗法公式と確率変数の依存関係から導き出せます。3行目も乗法公式を利用すれば導出できます。3行目を確認すると、1時刻先の平滑化分布p(x_{t+1 | y_{1:T}})とシステムモデル p(x_{t+1} | x_t)、予測分布 p(x_{t+1} | y_{1:t})、フィルタ分布 p(x_t | y_{1:t})から平滑化分布 p(x_t | y_{1:T})が導出できることがわかります。これらを図で表現すると以下のようになります。

f:id:hippy-hikky:20201105003816p:plain

固定ラグ平滑化

上記のようにして平滑化分布を導出できることがわかりましたが、実際に計算するとなると時刻Tまでの予測分布とフィルタ分布を記憶しておき、Tから順次計算する必要があります。

これを、一つの仮定を置くことで一度に計算しようとするアプローチが固定ラグ平滑化です。

固定ラグ平滑化では、時刻tの状態は、t+kまでの情報にのみ影響されるとします。平滑化とは、未来の情報を利用して、時刻tの予測を修正しようとするものです。影響範囲をk時刻先までに限定するということになります。つまり、あまり未来の情報は影響力は0では無いがとても小さいだろうと見做します。


\begin{align}
  p(x_t | y_{1:T}) \approx p(x_{t} | y_{1:t+k})
\end{align}

この仮定をおくと、状態をちょっと拡張するだけでフィルタと同時に平滑化が実行できます。

状態x_tはこれまで、t時刻の状態だけとしていましたが、t-kまでの状態を状態に含めます。


\begin{align}
  \tilde{x}_t \equiv [ x_t, x_{t-1}, x_{t-2}, \cdots, x_{t-k} ]^T
\end{align}

この拡張状態ベクトルを利用するとシステムモデルは次のように書けます。

f:id:hippy-hikky:20201105010505p:plain:h100

ここでαとした部分は、拡張する前のシステムモデルが入ります。 観測モデルも同様です。

このように拡張した状態ベクトルを利用することで、フィルタ分布を導出する際に同時にk幅のフィルタ分布を得ることができます。

固定点平滑化

固定ラグ平滑化では、k幅前の状態を順次拡張状態ベクトルとしていましたが、ある固定された時点の状態を状態ベクトルに取り込むことも可能です。初期状態x_0を取り込んで、事前分布の更新などに利用する例が「予測にいかす統計モデリングの基本」に書かれていました。

【トップに戻る】

パラメータ推論：自己組織型状態空間モデル

固定点平滑化について、ある固定点の状態ではなく、モデルパラメータ\thetaを状態ベクトルに含めることを考えます。

すると、時刻tまでの状態を推定する中で一緒にパラメータの事後分布p(\theta | y_{1, \cdots, t})が得られることになります。このように、パラメータを取り込むように拡張された状態空間モデルを「自己組織型状態空間モデル(Self-Organizing State Space Model)」と呼ぶらしいです。

f:id:hippy-hikky:20201105011510p:plain

前回は、グリッドサーチでハイパーパラメータを変えて何度も計算を行っていたので、計算にだいぶ時間がかかってしまいました。一方自己組織型状態空間モデルでは、フィルタ処理を行う中で同時にパラメータの事後分布が更新されていくので、データが増える毎にパラメータが新たな情報を取り込んでいきます。

パラメータの初期状態によっては初期の状態予測の精度があまりよくないだろうということは想像できます。しかし、グリッドサーチする計算量を考えたら、メリットの方が大きいかなと感じます。データの標本統計量などを利用してある程度のあたりをつけておくことも可能なので、そんなに外れた状態から開始するということも考えにくいですし。

次の章では実際に自己組織型状態空間モデルを実装して、状態推定と同時にモデルパラメータの推論を同時に行ってみます。状態推定の実際の計算にはパーティクルフィルタを利用します。

【トップに戻る】

自己組織型状態空間モデルの実装

問題設定

自己組織型状態空間モデルを試してみるために、第1回、第2回で利用したものと同じデータ(下記)を使います。

f:id:hippy-hikky:20201019095703p:plain
時系列データの例

モデリング

モデルとしては、第1回で扱った1階差分モデルを扱います。


\begin{align}
  x_t &\sim p(x_t | x_{t-1}) = \mathcal{N}(x_t | x_{t-1}, \alpha^2\sigma^2) \\
  y_t &\sim p(y_t | x_t)  = \mathcal{N}(y_t | x_{t}, \sigma^2)
\end{align}

状態x_tが1次元のシンプルなモデルです。

このモデルのパラメータは、\theta = \{\alpha, \sigma\}の二つです。このパラメータを状態に追加して拡張状態ベクトルを作りますが、\{\alpha, \sigma\}は正の値の必要があります。そこで、対数をとった値をパラメータとして推論することにします。（分布を適切に選定すれば良いのだと思いますが、参考にした資料でやっていたので。）


\begin{align}
  \theta = [ \log \alpha, \log \sigma]^T
\end{align}

\thetaが従う確率モデルはそれぞれ独立なガウス分布とします。

実装

以上のモデルを実装します。実装の詳細は以下のnotebookを参考にしてください。なお、パーティクルフィルタの実装については第1回を参照してください。

notebookをみてもらえれば分かると思いますが、状態を拡張しただけであとは第1回でもやったパーティクルフィルタの状態推定そのものとなっています。

推論結果

推論結果は以下のようになりました。

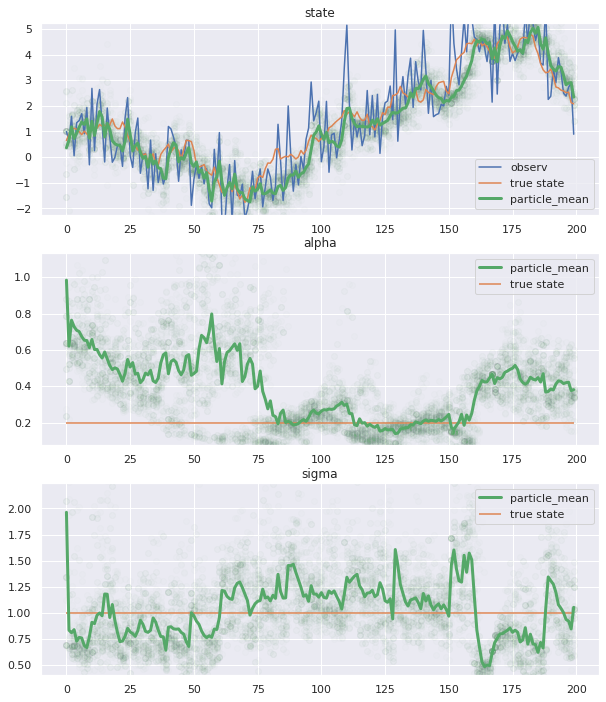
f:id:hippy-hikky:20201106212212p:plain
推論結果．上から時系列状態，αの事後分布，σの事後分布．オレンジ線が設定値，緑の実線は事後分布の平均．緑の点はパーティクルを示す．

上段の状態推定と同時にパラメータを推論しています。この結果からは、あまり初期の推論状態が悪いかどうかはわかりにくいですが、パラーティクルのばらつきが多いような気もします。

中下段のパラメータの推論状態をみると、初期状態から徐々に設定値に近づいているように見えます。（が、これであってますかね？？）

【トップに戻る】

おわりに

ということで、状態空間モデルのハイパーパラメータを自己組織化状態空間モデルを用いて推論してみました。

固定ラグ平滑化、固定点平滑化は状態ベクトルを変更するだけで状態推論と同時に平滑化まで実装できるというのはすごく楽ですね。アルゴリズム的にもめちゃくちゃシンプルで使いやすそうです。

ただ、正直実装があっているかどうかは自信がない部分があります。特に拡張状態ベクトルにおけるシステムモデルあたりが。

「予測にいかす統計モデリングの基本」を見ると、拡張した状態部分は恒等写像になっているのですが、パーティクルフィルタで推論する場合、状態がランダムに動かないと推論できないわけで。。。このあたりの理解が十分ではないなと感じてます。

気になった方、指摘いただけると助かります。

【トップに戻る】

参考資料

【トップに戻る】