ベイズ推論により混合分布のパラメータ推論をやってみる　〜線形回帰モデルの混合〜

回帰モデルは、データ $Y$ がデータ $X$ と確率変数 $W$ に依存する構造です（下図）。 $X$ を説明変数、 $Y$ を目的変数、 $W$ を重みパラメータなど呼ぶことが多いかもしれません。また、データ $X$ をそのまま使うのではなく、n次関数などのなんらかの関数 $\phi(X)$ を通すことも多いですね*2。このような操作を特に「特徴抽出」と呼んだりします。

f:id:hippy-hikky:20200313213335p:plain:w250

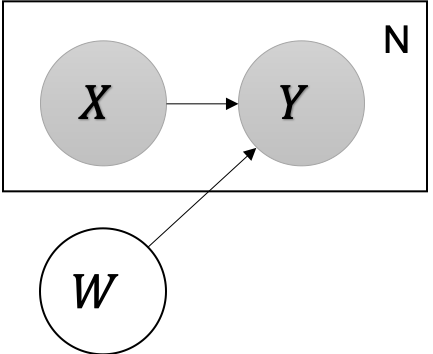
データ $(X,Y)$ はN個のペアとして与えられるもので、未知の変数 $W$ を $(X,Y)$ のペアに基づいて推論することが目的です。

$Y$ は $W$ と $X$ のなんらかの関数 $f(W,X)$ を平均としたガウスノイズが付加されて観測されるものとします*3。 $f(W,X)$ は、 $X$ にM個の関数 $\phi(\cdot)$ を通して得られる値と $W=\{w_0, w_1, \cdots, w_M\}$ の線型結合とします。

f:id:hippy-hikky:20200313214346p:plain:h100

$W$ が推論できれば、未知の入力変数 $x_*$ に対する $p(y_* | x_*, W, X, Y)$ を推論することができます。

線形回帰のベイズ推論については、解析解を求めることができます。詳しくは下記参考資料を参照してください。弊ブログでもソースコード付きで記事を公開していますので、興味があればこちらもご覧ください。

learning-with-machine.hatenablog.com

本記事では、MCMC アルゴリズムを利用して近似解を推論します。また、MCMC アルゴリズムはPyMC3を利用します。

パラメータ推論とその結果

ソースコード全文は添付のnotebookに掲載しています。必要な方は是非参照ください。

前回のガウス混合分布の推論でも書きましたが、PyMC3では確率モデルを上記のようにグラフィカルモデルなどで書けてしまえば、あとは、その確率変数の関係性を並べていくだけです。線形回帰モデルの定義部分は下記の通りです*4。

with pm.Model() as model_lr:
    tau = pm.Gamma('tau', alpha=1.0, beta=0.1)
    ws = pm.Normal('w', mu=0, tau=0.1, shape=nd+1)
    y = pm.Deterministic('y', pm.math.dot(ws, sample_x_feature))
    y_obs = pm.Normal('y_obs', mu=y, tau=tau, observed=sample_y)

登場する確率変数の確率分布を定義しているだけですね（めっちゃ簡単）。

細かくはnotebookを見ていただくとして、結果だけ示します。

f:id:hippy-hikky:20200313215527p:plain — 線形回帰モデルのベイズ推論の結果．グレーの線は事後分布からサンプルした関数を描画したもの．赤線は関数の推論結果(期待値)．青い線で設定値を描画．オレンジの点が学習データ．

真の関数として、二次関数を設定値として、そこから10点サンプルデータを取得しています(上図のオレンジの点)。二次関数からサンプルデータを取得しましたが、今回はちょっとイジワルで3次関数をフィッティングしてみました。

データが得られている領域はグレーの線が密集していますが、0未満や6付近は学習データが存在していないので、推論結果(グレーの線)がバラついており、予測の不確かさが現れています（それでも期待値はだいたい設定通り）。

【トップに戻る】

混合線形回帰モデル

前回の記事で混合モデルを扱いましたが、混合モデルは単純な確率分布の混合だけではないということを前回の記事でも書きました。混合モデルとは、コンポーネント(混合要素)を潜在変数 $s$ でスイッチングする構造を持ったモデルであり、非常に柔軟なモデルです。

ここでは、複数の線形モデルを組み合わせて、トレンドが複数あるデータのモデリングをやってみます。

グラフィカルモデルとしては、前回の混合モデルと上記の線形モデルを組み合わせただけですので、以下の通りです。

f:id:hippy-hikky:20200313220743p:plain

確率モデルを具体的に以下のように定義します。

f:id:hippy-hikky:20200313221609p:plain:h250

それぞれの確率変数に分布を設定しているだけで、特に難しいことはやっていません。一点だけ注意ですが、以下の実際の推論では、コンポーネントの割り当てを決める変数 $s$ を周辺化除去し、計算を効率化しています。この点について詳しくは前回の記事を参照してください。PyMC3では、MixtureというAPIが用意されており、このAPIを利用すれば、勝手に $s$ の周辺化除去をやってくれます。