ベイズ線型回帰：解析解の導出

【概要】

ベイズ推論による線型回帰問題の解析解の導出をなるべく丁寧に解説しているつもり（手書きでごめんなさい）
MAP値、予測分布、最尤推定解をそれぞれ比較してみる

【目次】

はじめに
線型回帰
実装
まとめ
参考文献

はじめに

本記事では、線型回帰問題を題材にベイズ的に予測分布の推論をやってみます。

当ブログでは、ベイズ線型回帰についてはこれまでもいくつか扱っています。ギブスサンプリングを利用した近似推論については「サンプリングによる近似ベイズ推論その3（MCMC:ギブスサンプリング） - 機械と学習する」で扱いました。また、「変分推論による近似ベイズ推論 - 機械と学習する」では、変分推論を利用して近似解の推論を行いました。また、PPL（確率プログラミング言語）の一つであるPyMC3を利用した推論として「ベイズ推論により混合分布のパラメータ推論をやってみる〜線形回帰モデルの混合〜 - 機械と学習する」のような記事もあります。これらはベイズ的な線型回帰の近似解の推論についてでしたが、「ベイズ線形回帰（解析解）の実装 - 機械と学習する」では、事後分布の解析解を導出しました。しかし、導出過程は別の書籍を案内するだけでした。また、予測分布については扱っていませんでした。そこで本記事では、ベイズ的な線型回帰のパラメータの事後分布の導出、予測分布の導出、MAP推定、最尤推定についてなるべく丁寧に導出過程を示すつもりです（手書きのメモを貼ってるだけですが。。。）。

ちなみに、以下のセミナーで話した内容を整理したものです。

liberal-arts-for-tech.connpass.com

なおここでの話題は、こちらのテキストでも取り扱っています（宣伝）。

【トップに戻る】

線型回帰

本記事では、「線形基底関数モデル*1」を扱います。多項式回帰のような特徴抽出処理も含めた一般形です。

線形基底関数モデル

回帰の問題は $y=ax+b$ という形式が中学くらいで出てくる最もシンプルな形式です。しかし、このモデルだけでは単純な直線しか表現できないので、この形を一般化して様々な状況で扱えるようなモデルに定式化します（線形基底関数モデル）。

グラフィカルモデルで表現すると以下のとおりです。

f:id:hippy-hikky:20200313213335p:plain:w300 — 回帰問題のグラフィカルモデル．グレーのノードは所与とする確率変数．

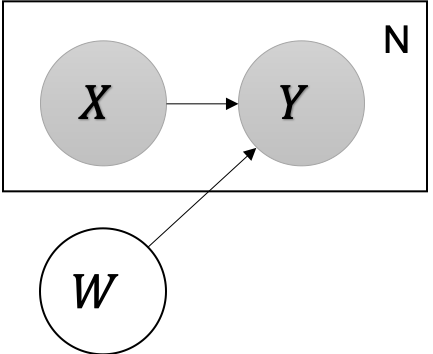
YはXとWに依存するという構造を示しています。また、X, YのペアはN個与えられ、Wが未知のパラメータであることも示しています。つまり、データ(X,Y)に基づいて、Wを推論することが目的となります。

このモデルの同時分布は以下の通りです。

${ \displaystyle \begin{eqnarray} p(\mathbf{w}, \mathbf{Y} | \mathbf{X}) = p(\mathbf{w})p(\mathbf{Y} | \mathbf{X}, \mathbf{w}) = p(\mathbf{w}) \prod^{N}_{n=1} p(y_n | \mathbf{x}_{n}, \mathbf{w}) \end{eqnarray} }$

今回は、変数Xを基底関数 $\mathbf{\phi}(x)=\{\phi_1(x), \phi_2(x), \cdots, \phi_M(x)\}^{T}$ で変換し、重みWと線型結合するモデルを考えます。基底関数での変換は「特徴抽出」と呼ばれることもあります。

具体的に、Yが従う確率分布を以下のように定義します。

${ \displaystyle p(y_n | \mathbf{x}_{n}, \mathbf{w}) = \mathcal{N}(y_{n} | \mathbf{w}^{T}\phi(\mathbf{x}_n), \sigma^{2}_{y}) }$

wが従う分布は以下の通りとしました。

${ \displaystyle p(\mathbf{w}) = \mathcal{N}(\mathbf{w} | \mathcal{0}, \sigma^{2}_{w}\mathbf{I}) }$

事後分布の導出

まずは、未知の変数wの事後分布を導出します。

確率モデルで未知の変数の確率分布を推論するには、確率モデルから知りたい変数についての分布を考えます。

${ \displaystyle \begin{eqnarray} p(\mathbf{w} | \mathbf{Y}, \mathbf{X}) \propto p(\mathbf{w})p(\mathbf{Y} | \mathbf{X}, \mathbf{w}) \end{eqnarray} }$

条件付き確率と同時確率の性質から自然に導出されます。あとはこのまま式を展開していくことで事後分布を自然に導出することができます。

導出した結果、事後分布は以下の通りとなります。

f:id:hippy-hikky:20200702003742p:plain:w300

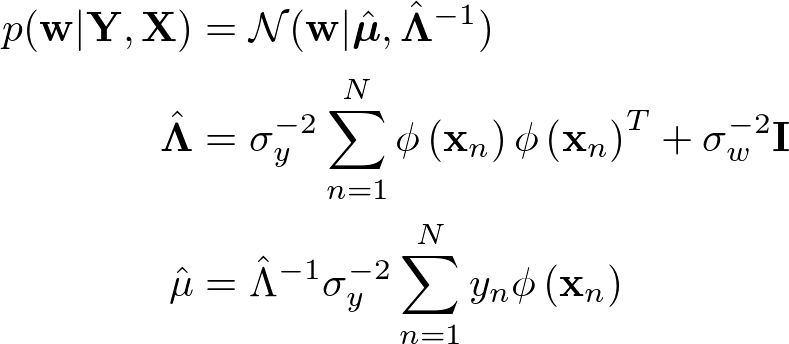
また、計画行列という以下で定義する行列を利用して書き直すと計算がよりシンプルになるので書き直してみます。

計画行列

f:id:hippy-hikky:20200702004424p:plain:w300

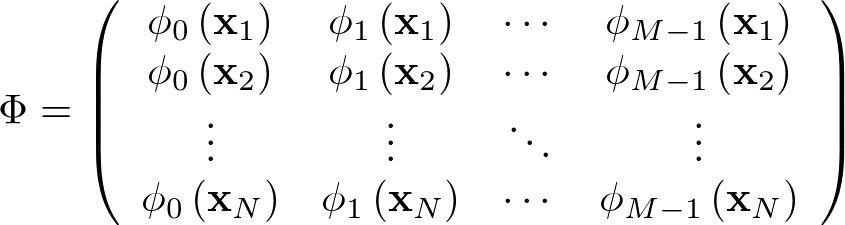
書き直した結果は以下のとおりです。

f:id:hippy-hikky:20200702005123p:plain:w200

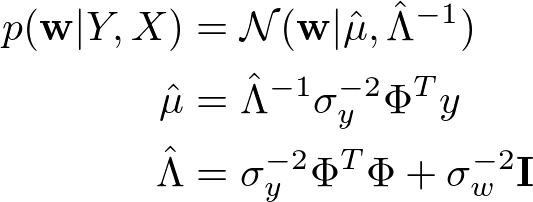
これらの導出過程を手書きですが添付しておきます。

drive.google.com

MAP推定

上記の設計での事後分布は、ガウス分布となることがわかりました。そのため、MAP(Maximum A Posterior)推定値はガウス分布の平均( $\hat{\mu}$ )です。

最尤推定

続いて、最尤推定解も導出します。

最尤推定では、尤度( $p(X, Y | w)$ )を最大化するwを導出します。導出の結果は上記の計画行列 $\Phi$ を利用して以下の通りとなります。

f:id:hippy-hikky:20200702005912p:plain:w200

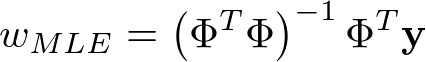
こちらの導出過程は以下に添付のとおりです。

f:id:hippy-hikky:20200702010008j:plain:w300

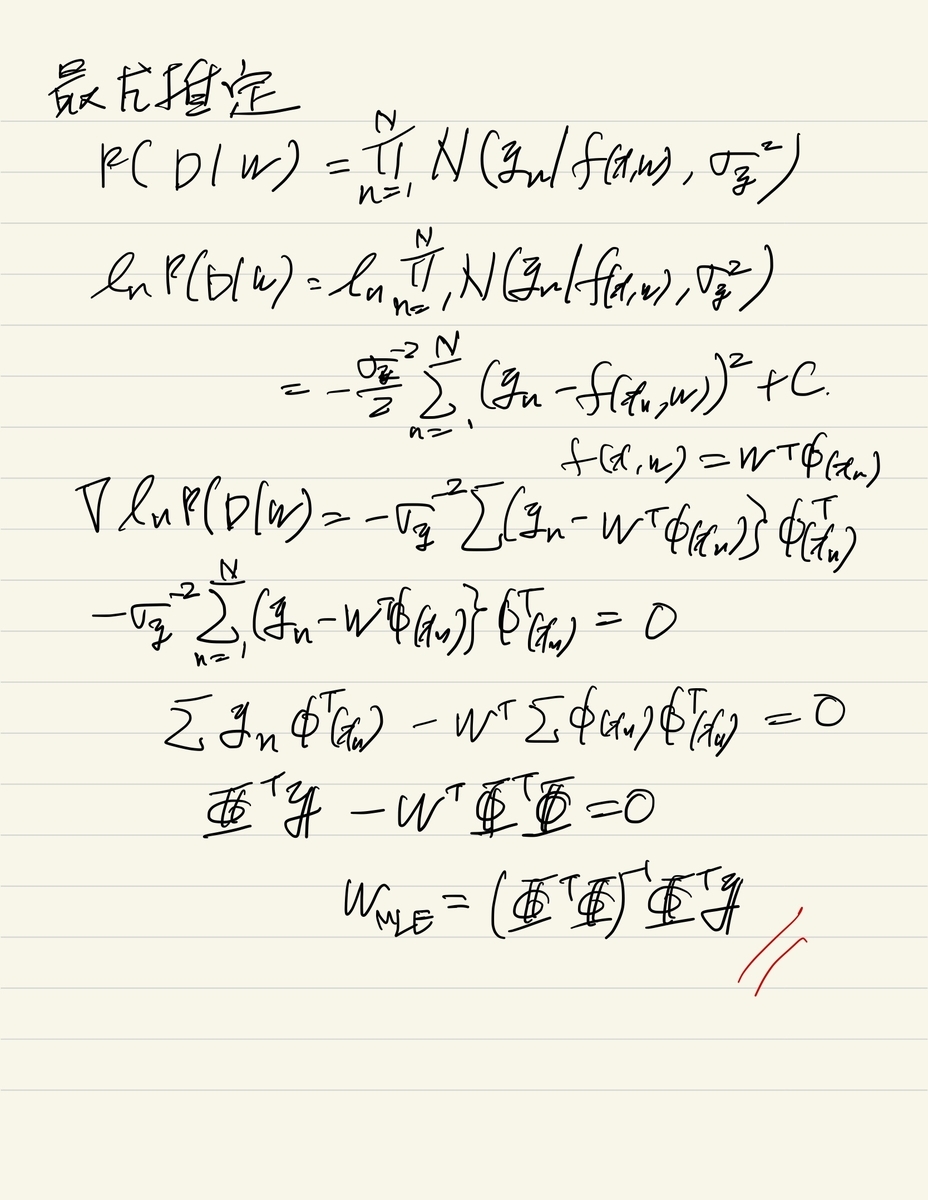
予測分布の導出

最後に、wの事後分布 $p(\mathbf{w} | X, Y)$ を利用して、未知のデータ[tex:(x*, y)]に対する予測分布[tex:p(y_ | x_*, Y, X)]を導出します。

こちらの導出は、ガウス分布の周辺分布となるので、PRMLのSec.2にある式を利用して導出します。

f:id:hippy-hikky:20200702010733p:plain:w400

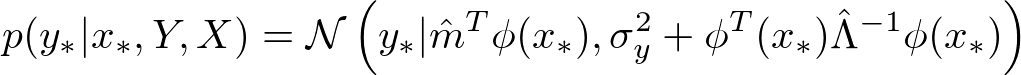
簡単ですが、こちらも導出過程を添付しておきます。

f:id:hippy-hikky:20200702010833j:plain:w300

【トップに戻る】

実装

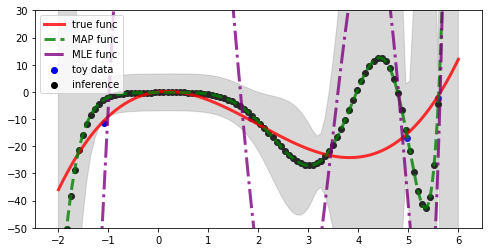
これらの線型回帰の推定値を比較してみます。詳細は以下に添付のnotebookを確認してください。添付のnotebookは、基底関数に多項式を使った場合の実装例です。notebookでは、3次の多項式の設定でデータ数が5つしか得られていない場合に、10次の多項式回帰モデルを適用した例となっています。

モデルの次数>データ数の場合に、最尤推定解は過剰適合するケースが多いですが、MAP推定値は比較的なめらかに関数を推論できているケースがあります（目立ったわかりやすい例はそんなに頻繁には出てこないですが）。

f:id:hippy-hikky:20200703000048p:plain — 線形回帰（多項式回帰）の予測結果．赤線が設定値．青点は赤線の関数からサンプルした点．緑線がMAP推定値．紫線が最尤推定値を示している．

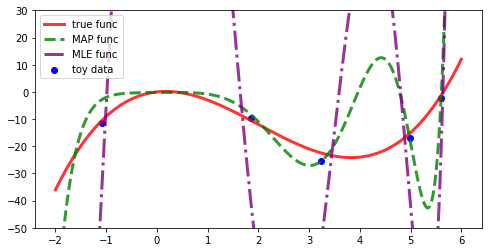
予測分布については、データが疎らな領域の分散が大きくなっていることがわかります。

f:id:hippy-hikky:20200703000303p:plain — 上図に予測分布（グレー領域）を重ねた結果．

【トップに戻る】

まとめ

ということで今回は、線形回帰（基底関数モデル）の推論をベイズ的に行い、最尤推定量との差異を比較してみました。

推論結果を確認すると、データが少ない領域での予測分布の分散の広がりが定量的に扱えることや、過学習が自然に抑えられていそうだというメリットがわかりました。

今回は線型回帰なので、（簡単とは言えないが）解析解を導出することができました。しかし一般には、解析的に事後分布や予測分布を導出できることは保証されていません。そのため、MCMCなどの近似推論が使われます。MCMCによって事後分布のサンプルを得ることができれば、予測分布もモンテカルロ積分すれば良いのでコンピュータとの相性も良いです。解析解を利用して予測分布を導出よりも計算量はかかりますが、人手で計算する時間と手間を考えればガチガチにパフォーマンスを求められるようなアプリケーションじゃなければ十分じゃないかと思ったり思わなかったり。

なお、MCMC アルゴリズムについては、参考文献[須山2017, ビショップ2007]あたりを見ることが一番の近道だと思います。

【トップに戻る】