変分推論による近似ベイズ推論

【概要】

ベイズ推論について実装して理解するシリーズ
今回は、変分推論を使って近似ベイズ推論を行ってみます
適用例として、ガウス分布のパラメータ推論と線形回帰を近似推論してみました

【目次】

はじめに
変分推論
- 変分推論による近似ベイズ推論
変分推論による近似ベイズ推論の実装
- 実装例1：1変数ガウス分布のパラメータ推論
  - モデル
  - 実装結果
- 実装例2：線形回帰のパラメータ推論
実装コード全体
おわりに
参考文献

はじめに

ベイズ推論についての書籍を読んでいると、なんとなく理解はできても具体的なイメージがわかないことないですか？
ということで、実装して理解を深めていきたいと思います。

本記事ではベイズ推論における近似推論について扱います。ベイズ推論では「MCMC(Markov Chain Monte Carlo)法」などのサンプリングに基づくアルゴリズムと「変分推論」という代表的な近似推論手法があります。

サンプリングに基づく近似ベイズ推論(MCMC)について、過去3回に分けて書いてきました。その1では、基本的な積分の近似計算である「モンテカルロ積分」と最も単純なサンプリングアルゴリズムである「棄却サンプリング」を実装しました。その2では、MCMC アルゴリズムの一種である「メトロポリス法」を実装しました。その3では、同じくMCMC アルゴリズムの一種であるギブスサンプリングを実装してみました。

今回は、サンプリングをベースとした近似アルゴリズムとは異なる、平均場近似を使った変分推論を実装してみます。

本記事は、「ベイズ深層学習」の「4章近似ベイズ推論」を参考にしています。

ベイズ深層学習 (機械学習プロフェッショナルシリーズ)

作者:須山敦志
発売日: 2019/08/08
メディア: 単行本

間違いなどあったら指摘していただけると助かります。

【トップに戻る】

変分推論

ベイズ推論において、パラメータの推論が解析的に行えないケースがあります。例えば、確率変数が非線形な関係にあるとか、確率変数同士が共役関係にないなどの場合です。このような場合には近似的に推論を行う必要があります。

ベイズ推論でよく使われる近似推論手法として、大きく分けて以下の二つの手法があります。

MCMC：サンプリングに基づく推論
変分推論：最適化に基づく推論

ここでは変分推論によって近似ベイズ推論を実装してみようと思います。

変分推論による近似ベイズ推論

変分推論の詳細は、PRML(下)やベイズ深層学習などを参照ください*1。

長くなってしまったので詳細はクリックで展開

観測変数を $\mathbf{X}=\{\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_N\}$ 、潜在変数を $\mathbf{Z}=\{\mathbf{z}_1, \mathbf{z}_2, \cdots, \mathbf{z}_N\}$ とすると、モデルは $p(\mathbf{X}, \mathbf{Z})$ となります。ベイズ推論では、データ $\mathbf{X}$ に基づいて潜在変数 $\mathbf{Z}$ の事後分布 $p(\mathbf{Z} | \mathbf{X})$ を求めることが目的です。

ここでは事後分布 $p(\mathbf{Z} | \mathbf{X})$ が解析的に求められない場合を考えます。そこで、事後分布 $p(\mathbf{Z} | \mathbf{X})$ を素性のわかっている関数 $q(\mathbf{Z} ; \xi)$ で近似することを考えます。 $p(\mathbf{Z} | \mathbf{X})$ と $q(\mathbf{Z} ; \xi)$ が近い（近似できている）とする指標として、KLダイバージェンス(Kullback-Leibler Divergence)を使います。

${ \displaystyle \begin{eqnarray} \mathrm{KL} [q(\mathbf{Z} ; \xi) || p(\mathbf{Z} | \mathbf{X})] = - \int q(\mathbf{Z} ; \xi) \ln \frac{p(\mathbf{Z} | \mathbf{X})}{q(\mathbf{Z} ; \xi)} \end{eqnarray} }$

このKLダイバージェンスを最小化するように $q(\mathbf{Z} ; \xi)$ を求めれば良いのですが、事後分布 $p(\mathbf{Z} | \mathbf{X})$ が入っているので、これが計算できたら苦労しないわけです。最適化計算ができるような戦略を考える必要があり、まず、対数周辺尤度を次のように分解してみます*2。

${ \displaystyle \begin{eqnarray} \ln p(\mathbf{X}) = \mathcal{L}(\xi) + \mathrm{D_{KL}}[ q(\mathbf{Z} ; \xi) || p(\mathbf{Z} | \mathbf{X}) ] \end{eqnarray} }$

対数周辺尤度 $\ln p(\mathbf{X})$ は定数なので、 $\mathrm{KL} [q(\mathbf{Z} ; \xi) || p(\mathbf{Z} | \mathbf{X})]$ を最小化するということは、 $\mathcal{L}(\xi)$ を最大化するということになります。ここで、 $\mathcal{L}(\xi)$ は次のKLダイバージェンスです。

${ \displaystyle \begin{eqnarray} \mathcal{L}(\xi) = \mathrm{D_{KL}}[ q(\mathbf{Z} ; \xi) || p(\mathbf{X}, \mathbf{Z}) ] = \int q(\mathbf{Z} ; \xi) \ln \frac{p(\mathbf{X}, \mathbf{Z})}{q(\mathbf{Z} ; \xi)} \end{eqnarray} }$

$q(\mathbf{Z} ; \xi)$ は素性がわかっているとする関数ですし、 $p(\mathbf{X}, \mathbf{Z})$ は同時分布なのでどのような関数かわかります*3ので、このKLダイバージェンスなら計算できそうです。

事後分布を近似する関数 $q(\mathbf{Z} ; \xi)$ は、問題によっていくつか考えられるそうです。特に、潜在変数をM個に分割( $\mathbf{Z}=\{\mathbf{Z}_1, \mathbf{Z}_2, \cdots, \mathbf{Z}_{M}\}$ )し、それぞれ独立であると考えることが多いと思います*4。これを「平均場近似」と呼ぶそうです。

${ \displaystyle \begin{eqnarray} q(\mathbf{Z}) = \sum^{M}_{i=1} q(\mathbf{Z}_{i}) \end{eqnarray} }$

このように近似をすると、最大化させたいKLダイバージェンス $\mathcal{L}(\xi)$ は以下のように変形できます*5。

${ \displaystyle \begin{eqnarray} \mathcal{L}(\xi) = \mathrm{D_{KL}}[q(\mathbf{Z}_j ; \xi) || \exp\{\mathbb{E}_{i\neq j}(\ln p(\mathbf{X}, \mathbf{Z}) + \mathrm{const.}) \} ] \end{eqnarray} }$

ということで、潜在変数の部分集合 $\mathbf{Z}_j$ に対する最適関数は以下の通りとなります。

${ \displaystyle \begin{eqnarray} \ln q^{*}_{j}(\mathbf{Z}_j | \xi) = \mathbb{E}_{i\neq j}[\ln p(\mathbf{X}, \mathbf{Z})] + \mathrm{const.} \end{eqnarray} }$

これはj番目の潜在変数の集合の最適解となります。全体を最適化させるには、はじめに初期化を行い、ギブスサンプリングと同様に一つづつM個の関数を更新していきます。

【トップに戻る】

変分推論による近似ベイズ推論の実装

変分推論の適用例として二つの問題を実装してみます。これらは共に解析的に解を導くことができる問題ですが、練習として。

1変数ガウス分布のパラメータ推論
線形回帰のパラメータ推論

実装例1：1変数ガウス分布のパラメータ推論

モデル

N個のデータ $X=\{x_1, x_2, \cdots, x_N\}$ が得られており、このデータ $X$ は次のガウス分布 $\mathcal{N}(x_n|\mu, \tau^{-1})$ に従うものとします。

${ \displaystyle \begin{eqnarray} x_n \sim p(x_n | \Theta) = \mathcal{N}(x_n|\mu, \tau^{-1}) \end{eqnarray} }$

ここで、 $\mu$ は平均、 $\tau$ は精度(分散の逆数)を示すパラメータの確率変数です。

${ \displaystyle \begin{align} \mu \sim \mathcal{N}(\mu | \mu_0, (\lambda_0 \tau)^{-1}) \\ \tau \sim \mathrm{Gamma}(\tau | a_0, b_0) \end{align} }$

このようにモデルを設計すると、パラメータの事後分布は次のようになります。

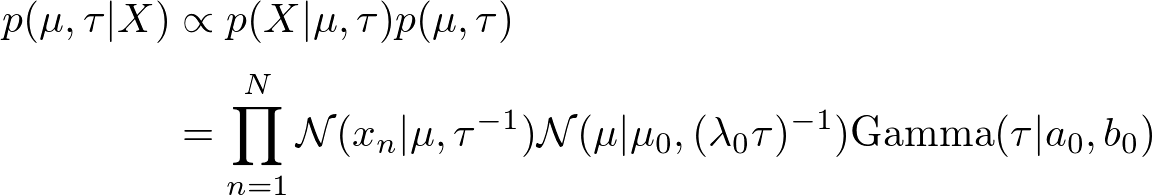
f:id:hippy-hikky:20191219000738p:plain:w500

ガウス分布と $\mu, \tau$ の分布は共役関係にあるので、この事後分布は解析的に導くことができます。ですがここでは練習として、次のように平均と精度を分解(平均場近似)して近似推論してみます。

${ \displaystyle \begin{align} q(\mu, \tau) = q(\mu)q(\tau) \end{align} }$

$\mu, \tau$ の最適関数は上述の式に当てはめて、展開して得ます。平均 $\mu$ に対する最適関数は以下のように展開できます。

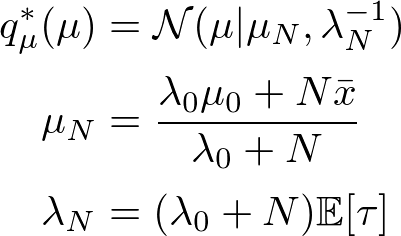
f:id:hippy-hikky:20191219001740p:plain:h100

精度 $\tau$ に対する最適関数も同様です。

f:id:hippy-hikky:20191219001851p:plain:h100

$\mu$ はガウス分布、 $\tau$ はガンマ分布になることがわかりました。

ここで、事前分布のパラメータを $\mu_0 = \lambda_0 = a_0 = b_0 = 0$ とすると $\mu$ の1次と2次のモーメントは次のようになります。

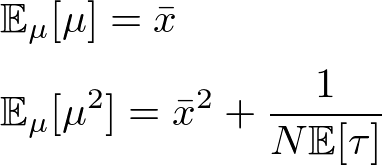
f:id:hippy-hikky:20191219003153p:plain:h60

この値を利用してガンマ分布のパラメータ $b_N$ を展開すると次の通りとなります。

${ \displaystyle \begin{align} b_N = \frac{N}{2}\left(\bar{x^2} - \bar{x}^2 + \frac{1}{N\mathbb{E}\left[\tau\right]} \right) \end{align} }$

なお、 $\tau$ の期待値は $\mathbb{E}[\tau] = \frac{a_N}{b_N}$ です。

実装結果

実装コードの全体は実装コード全体にnotebookを貼り付けているので参照してください。

まず、テスト用のデータとして、平均0, 精度0.5のガウス分布から100点のデータをサンプルしました。このデータを利用して推論を行います。

パラメータ推論は、適当に初期値を決めた $\mu, \tau$ それぞれの関数を順々に更新していきます。

def q_mu(X, tau_e):
    mean_x = X.mean()
    N = len(X)
    mu_n = mean_x
    lambda_n = N * tau_e
    return mu_n, lambda_n

def q_tau(X, tau_e):
    mean_x = X.mean()
    mean_x2 = (X**2).mean()
    N = len(X)
    a_n = (N + 1) / 2.
    b_n = (N / 2.) * (mean_x2 - mean_x**2 + (1. / (N*tau_e)))
    return a_n, b_n

tau_e = 1.0
taus = [tau_e]
n_iter = 10
for i in tqdm(np.arange(n_iter)):
    # q(mu)
    mu_n, lambda_n = q_mu(X, tau_e)
    # q(tau)
    a_n, b_n = q_tau(X, tau_e)
    # E[tau]の更新
    tau_e = a_n / b_n
    taus.append(tau_e)

q_mu(), q_tau()がそれぞれ平均と精度の関数です。先に展開したモデルからtau_e（ $\mathbb{E}[\tau]$ ）が更新すべきパラメータです。

$\mathbb{E}[\tau]$ の更新系列は、以下のようにすぐにほぼ最適解に収束したようです。

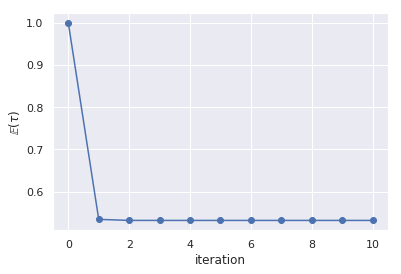
f:id:hippy-hikky:20191219005839p:plain

平均と精度の事後分布は以下のように推論できました。

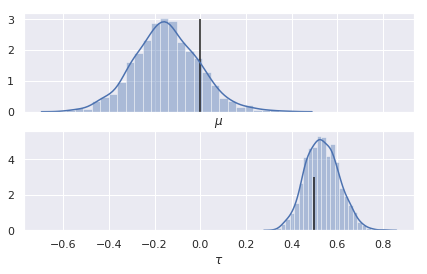
f:id:hippy-hikky:20191219010109p:plain — 平均(上)と精度(下)の近似事後分布．グレーの線は設定値(真値)を表す．

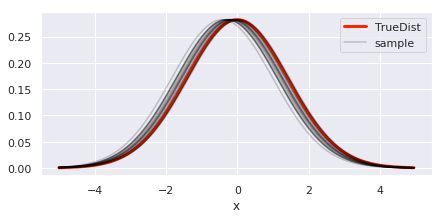
この結果を利用して、事後分布からパラメータをサンプルしてガウス分布を描いてみました。設定値（真の分布）とほとんど同じ分布を推測できていることがわかります。

f:id:hippy-hikky:20191219010427p:plain — 推論したガウス分布．赤が設定値，グレーが事後分布からサンプルした20本の予測分布．

実装例2：線形回帰のパラメータ推論

前節ではガウス分布のパラメータを推論しました。本節ではもう少しモデルを複雑にして、線形回帰モデルのパラメータ推論を変分推論します*6。

モデル

線形回帰モデルのグラフィカルモデルは以下のものになります。

f:id:hippy-hikky:20191204105503p:plain:w350 — 線形回帰のグラフィカルモデル．Wはデータに依存しないパラメータ(重み係数)．

線形回帰なので、この問題は解析解を得ることができます。また、前回の記事では同じ問題をギブスサンプリング (MCMC アルゴリズムの一つ)で推論しました。よければこちらも参照ください。本記事では解析解の導出は扱わないので。

learning-with-machine.hatenablog.com

まずはモデル（同時分布）を構築します。

${ \displaystyle \begin{eqnarray} p(\mathbf{w}, \mathbf{Y} | \mathbf{X}) = p(\mathbf{w})p(\mathbf{Y} | \mathbf{X}, \mathbf{w}) = p(\mathbf{w}) \prod^{N}_{n=1} p(y_n | \mathbf{x}_{n}, \mathbf{w}) \end{eqnarray} }$

今回は、変数Xの1次の線形回帰モデルを扱います*7。

${ \displaystyle \begin{eqnarray} p(y_n | \mathbf{x}_{n}, \mathbf{w}) = \mathcal{N}(y_{n} | \left(w_0+w_1x \right), \sigma^{2}_{y}) \end{eqnarray} }$

ここで簡単のために、分散 $\sigma^{2}_{y}$ は固定のパラメータとします。

重み $\mathbf{w}=\{w_0, w_1\}$ は未知の確率変数であり、これにも何らかの確率分布を仮定する必要があります。そこで、重み $\mathbf{w}$ はガウス分布に従うとし、事前分布として平均0で分散 $\sigma^{2}_{w}$ を与えることにします*8。なお、分散 $\sigma^{2}_{w}$ は固定のパラメータとします。

${ \displaystyle \begin{eqnarray} p(\mathbf{w}) = \mathcal{N}(\mathbf{w} | \mathcal{0}, \sigma^{2}_{w}\mathbf{I}) \end{eqnarray} }$

以上の設定で、データ $\mathcal{D}=\{\mathbf{X}, \mathbf{Y}\}$ を観測した後での重み $\mathbf{w}$ に関する事後分布 $p(\mathbf{w} | \mathbf{X}, \mathbf{Y})$ を求めることが目的です。

変分近似

変分推論を適用するにあたり、重み $\mathbf{w}=\{w_0, w_1\}$ をそれぞれ別々に近似していきます。

${ \displaystyle \begin{eqnarray} p(\mathbf{w}|\mathbf{X}, \mathbf{Y}) \simeq q(w_0)q(w_1) \end{eqnarray} }$

前章で求めた通り、潜在変数 $Z_i$ の最適解は以下の通りです。

${ \displaystyle \begin{eqnarray} \ln q^{*}_{j}(\mathbf{Z}_j | \xi) = \mathbb{E}_{i\neq j}[\ln p(\mathbf{X}, \mathbf{Z})] + \mathrm{const.} \end{eqnarray} }$

これに線形回帰のモデルを当てはめると、 $\{w_0, w_1\}$ それぞれの最適解は以下のようになります。

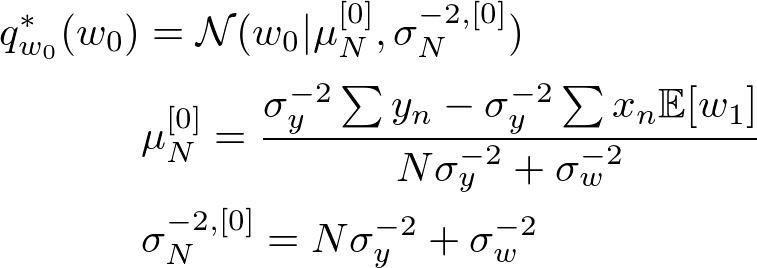
f:id:hippy-hikky:20191219161828p:plain:h100

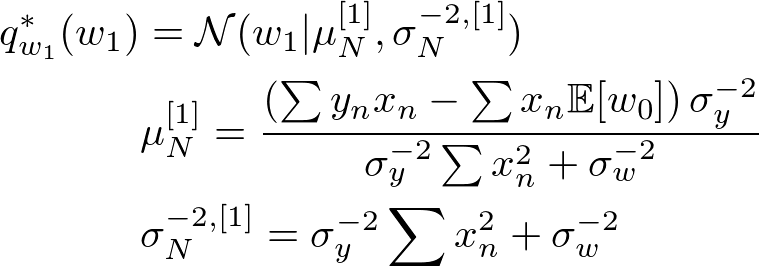
f:id:hippy-hikky:20201125002517p:plain:h100

あとはガウス分布のパラメータ推論と同じで、初期値を決めて、それぞれ更新していきます。

実装結果

こちらも実装コードの全体は実装コード全体にnotebookを貼り付けているのでそちらを参照ください。

真の関数として $y = 1.5x+0$ の関数を設定しました。ノイズはガウス分布として、分散 $\sigma^2_y$ を1.0に設定しました。この関数から20点のデータをサンプルし、線形回帰のパラメータを推論します。

推論に関するコードは以下の通りです。

def q_w0(X, Y, e_w1, sig2_y, sig2_w):
    sig2_y_inv = 1.0 / sig2_y
    sig2_w_inv = 1.0 / sig2_w
    N = len(X)
    sig2_n_inv = N*sig2_y_inv + sig2_w_inv
    sig2_n = 1.0 / sig2_n_inv
    mu_n = (np.sum(Y) - np.sum(X)*e_w1) * sig2_y_inv * sig2_n
    return mu_n, sig2_n

def q_w1(X, Y, e_w0, sig2_y, sig2_w):
    sig2_y_inv = 1.0 / sig2_y
    sig2_w_inv = 1.0 / sig2_w
    N = len(X)
    sig2_n_inv = sig2_y_inv * (sample_x**2).sum() + sig2_w_inv
    sig2_n = 1.0 / sig2_n_inv
    mu_n = (np.sum(Y * X) - np.sum(X)*e_w0) * sig2_y_inv * sig2_n
    return mu_n, sig2_n

e_w0, e_w1 = 0.0, 0.0

var_w = 0.1
n_iter = 20
mu0s = [e_w0]
mu1s = [e_w1]
for i in tqdm(np.arange(n_iter)):
    # q_w0
    mu0_n, var0_n = q_w0(sample_x, sample_y, e_w1, var_y, var_w)
    e_w0 = mu0_n
    # q_w1
    mu1_n, var1_n = q_w1(sample_x, sample_y, e_w0, var_y, var_w)
    e_w1 = mu1_n
    
    mu0s.append(mu0_n)
    mu1s.append(mu1_n)

$\{w_0, w_1\}$ それぞれの最適解をq_w0、q_w1という関数で実装しています。初期値を設定してこの二つの関数の推論を繰り返して行くだけです。

今回は式展開を簡単にするために、1次回帰モデルしか扱えないものにしましたが、ギブスサンプリングを実装した記事でやったように基底関数モデルにすることで汎用性が高まります。また、上記のコードでq_w0、q_w1のようにそれぞれ関数を作っているのが冗長ですが、一般解が得られるはずです。

上記のコードを実行した結果、 $\{w_0, w_1\}$ の期待値がどのように収束していったかを確認してみます。

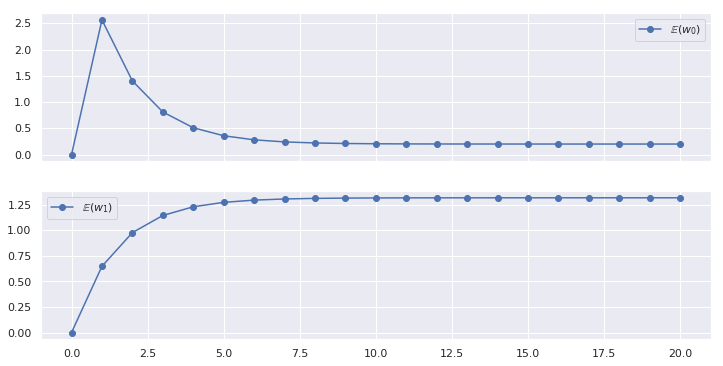
f:id:hippy-hikky:20191219163922p:plain — w0, w1のそれぞれの更新結果．上がw0，下がw1．

20回の更新の結果得られた事後分布は以下の通りです。

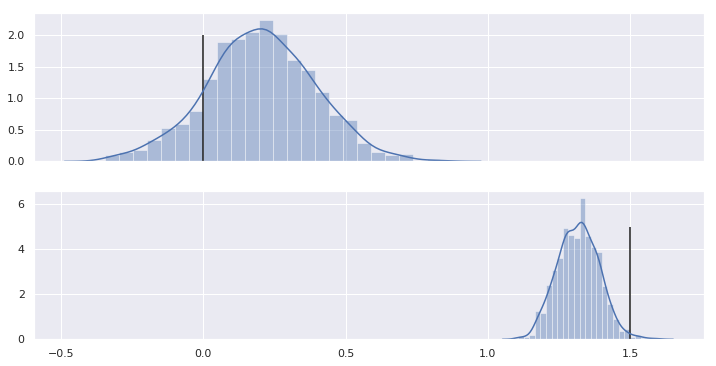
f:id:hippy-hikky:20191219164140p:plain — w0, w1のそれぞれの事後分布．

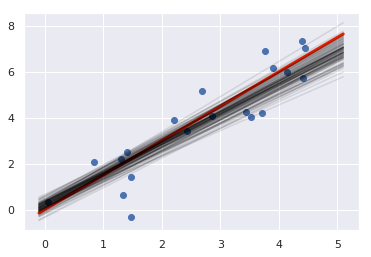
この結果を利用して、事後分布からパラメータをサンプルして推定した関数を描いてみます。設定値と同じような関数を推測できていることがわかります。

f:id:hippy-hikky:20191219164258p:plain — 推論した回帰式．赤は設定値(真の関数)，青点は真の関数から取得したデータ．グレーが事後分布からサンプルした20本の関数．

【トップに戻る】

実装コード全体

【トップに戻る】

おわりに

ということで、近似ベイズ推論アルゴリズムの一つ、変分推論を実装してみました。

メトロポリス法やギブスサンプリングと比較すると、関数を直接近似するのでサンプルを多量に得るという処理が要らなくなり、高速に推論ができます。
しかし、パラメータの事後分布が既知の関数として展開できない場合にはどのようにするのか、このあたりが私自身がよくわかっていません。引き続き学習を進めていきたいと思います。

何か気づいたことがあれば、ご指摘いただけると助かります。

【トップに戻る】