機械と学習する

統計解析、機械学習について学習したことをまとめていきます

トップ > 統計モデリング > 系列データの統計モデリング　〜カルマンフィルタ の導出と実装〜

系列データの統計モデリング　〜カルマンフィルタ の導出と実装〜

統計モデリング 系列データ カルマンフィルタ

【概要】

  • 系列データのモデリングと状態推定のシリーズ4回目
  • 今回は、カルマンフィルタ の導出と実装をやってみます

【目次】

はじめに

統計モデリングを行うにあたって、独立同分布(i.i.d; independent and identically distributed)を仮定することが多いと思います。

しかし、i.i.dを仮定できないケースはよくあります。時系列などの系列データが代表的です。また、i.i.dを仮定することが多い対象でも、計測対象や計測装置の経時的な変化（劣化）など本来的には系列を考慮しないといけない場面はあると思います。

系列データの解析について、主に「予測にいかす統計モデリングの基本」を参考に確認しましたので、数回に分けてまとめていこうと思います。なお、状態空間モデル(State Space Model)を使ったモデリングが対象です。

本シリーズここまでは、パーティクルフィルタを使った状態推定を行ってきました。状態空間モデルの推論についてパーティクルフィルタと同じかそれ以上に有名なものにカルマンフィルタがあります。今回は、カルマンフィルタを利用して時系列データの状態推定を行います。

間違いや勘違いなど、なにかありましたら指摘いただけるとすごく助かります。

No. リンク
第1回 系列データの統計モデリング 〜パーティクルフィルタによる状態推定〜 - 機械と学習する
第2回 系列データの統計モデリング 〜ハイパーパラメータの推定〜 - 機械と学習する
第3回 系列データの統計モデリング 〜自己組織型状態空間モデルを利用した状態推定モデルのハイパーパラメータ推定〜 - 機械と学習する
第4回 これ

【トップに戻る】

カルマンフィルタ

カルマンフィルタ とは

線形ガウス状態空間モデル(下記)における状態推定のためのアルゴリズムです。線形ガウス状態空間モデルとは、システムモデル、観測モデルが線形結合とガウスノイズで構成された状態空間モデルです。


\begin{align}
   x_t &= F_t x_{t-1} + v_t, c_t \sim \mathcal{N}(0, Q_t) \\
   y_t &= H_t x_t + w_t, w_t \sim \mathcal{N}(0, R_t)
\end{align}

第1回で紹介した一般状態空間モデルと比較すると、ベースとなる確率分布が限定されますので、ちょっと不便を感じるかもしれません。パーティクルフィルタはこの制限がなく、任意のモデルを適用することができます。

ただ、この制限を課すことで、フィルタ分布が解析的に導出できるので、推論に必要な計算が圧倒的に速いですし、安定した挙動を示します。ハイパーパラメータ*1の考慮もあまりないので使いやすいです。シビアなリアルタイム処理で効果を発揮する気がします(個人的な経験)。

なお本記事では、式のノーテーションは基本的に予測にいかす統計モデリングの基本に基づいています。後述の導出過程は確率ロボティクスを参考にしています。参考にしているというかほぼなぞっただけです。

アルゴリズムの導出

導出過程は確率ロボティクスを完全に信頼してなぞっています。とても丁寧に書かれており、すごくわかりやすいので、詳しく知りたい方は是非確率ロボティクスを参照してもらえたらと思います。カルマンフィルタだけでなく、パーティクルフィルタもわかりやすいです。移動ロボットのSLAMを題材にしていますが、状態空間モデルを確認したい場合にはとてもお勧めです。

状態空間モデルの状態推定についての基本は、第1回で記載の通り、予測分布[tex:p(x_t | y{1:t-1})]とフィルタ分布[tex:p(x_t | y{1:t})]を導出する必要があるのでした。


\begin{align}
   p(x_t | y_{1:t-1}) &= \int p(x_t | x_{t-1}) p(x_{t-1} | y_{1:t-1}) dx_{t-1} \\
   p(x_t | y_{1:t}) &= \eta p(y_t | x_t) p(x_t | y_{1:t-1})
\end{align}

線形ガウス状態空間モデルでは、上記のシステムモデル、観測モデルは多次元ガウス分布となるため、予測分布とフィルタ分布は定義に従って解析解を導出することができます。

導出の詳細は長くなってしまったので、本記事末にPDFを貼り付けておきます。手書きなのでだいぶ読めないと思いますので（ごめんなさい）、確率ロボティクスなどを参照されることを強くお勧めします。

結論だけを書くと、予測分布とフィルタ分布は以下のガウス分布となります。


\begin{align}
   p(x_t | y_{1:t-1}) &= \mathcal{N}(\bar{\mu}_t, \bar{\Sigma}_t) \\
      &\bar{\mu}_t = F_t \mu_{t-1} \\
      &\bar{\Sigma}_t = \left( Q_t + F_t \Sigma_{t-1} F^T_t \right)^{-1} \\
   p(x_t | y_{1:t}) &= \mathcal{N}(\mu_t, \Sigma_t) \\
     &\mu_t = \bar{\mu}_t + K_t \left( y_t - H_t \bar{\mu}_t \right) \\
     &\Sigma_t = \left[ \mathcal{I} - K_t H_t \right] \bar{\Sigma}_t \\
     &K_t = \bar{\Sigma}_t H_t^T \left( H_t \bar{\Sigma}_t H^T_t + R_t \right)^{-1}
\end{align}

アルゴリズム

アルゴリズムは上記のフィルタ分布（[tex:p(x_t | y{1:t})]）を導出するだけなので、モデルの定義に従って、[tex: \bar{\mu}t, \bar{\Sigma}_t, K_t, \mu_t, \Sigma_t]の順に求めていくだけです。

  1. 初期状態を適当に設定（\mathcal{N}(\mu_0, \Sigma_0)）
  2. input : \mu_{t-1}, \Sigma_{t-1}, y_t
    1. 予測分布の導出： \bar{\mu}_t, \bar{\Sigma}_tの計算
    2. フィルタ分布の導出： K_t, \mu_t, \Sigma_tの計算
  3. 2に戻って繰り返し

【トップに戻る】

実装

これまでのシリーズと同じ時系列のトイデータを使って状態推定してみます。

f:id:hippy-hikky:20201019095703p:plain
今回扱う時系列のトイデータ．線形ガウス状態空間モデルなので，カルマンフィルタ を適用できる．

このデータを次の状態空間モデルで推論します。


\begin{align}
  x_t &\sim p(x_t | x_{t-1}) = \mathcal{N}(x_t | x_{t-1}, \alpha^2\sigma^2) \\
  y_t &\sim p(y_t | x_t)  = \mathcal{N}(y_t | x_{t}, \sigma^2)
\end{align}

ということで、明らかに線形ガウス状態空間モデルですね。

実装と結果は下記に添付するnotebookに全コードを書いています。まぁ掲載するほどでもないですけどね。結果だけを載せておきます。

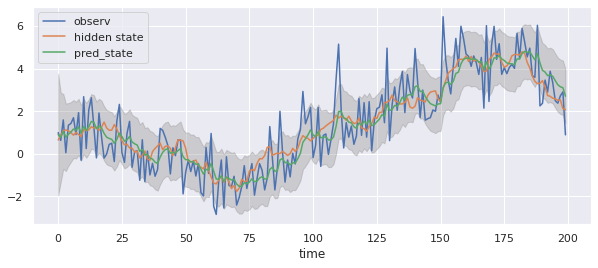
f:id:hippy-hikky:20201124142904p:plain
カルマンフィルタによる推論結果．青は観測値，オレンジは真の状態，緑線は推論結果(ガウス分布の平均)，グレーの領域は3σ範囲を示す．

全コードはこちらです。

カルマンフィルタクラスはこちらです。

【トップに戻る】

おわりに

ということで、カルマンフィルタの導出を確認し、時系列データの状態推定をに応用してみました。

推論結果多次元ガウス分布になるので、平均と共分散を計算するだけで推論ができます。そのため推論にかかる計算は短かったです。正確な比較をしていないですが、体感で明らかにパーティクルフィルタより速いです（まぁ当然ですが）。

しかし、導出結果だけを利用するなら別になんてことないのですが、フィルタ分布を導出しようとすると行列の計算がけっこう厳しいかったです。圧倒的に数学力が足りない。

次回はパーティクルフィルタとの比較をやってみようと思います。

気になった方、指摘いただけると助かります。

【トップに戻る】

参考資料

【トップに戻る】

*1:パーティクルフィルタではパーティクルの数が計算時間と精度のトレードオフです。これが結構厳しかったりするんですよね。GPU使って分散処理を適用できれば良いのですが、技術力の問題で。。。