機械と学習する

統計解析、機械学習について学習したことをまとめていきます

トップ > 統計検定準一級 > 【統計検定準一級】第8章 統計的推定の基礎 #2【番外編】

【統計検定準一級】第8章 統計的推定の基礎 #2【番外編】

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズの番外編
  • 8章「統計的推定の基礎」の内容をまとめます
  • 今回は推定法として「最尤法」と「モーメント法」について

【目次】

はじめに

「統計学実践ワークブック(参考資料1)」の問題を解いていくシリーズをやっていく中で、8章「統計的推定の基礎」の内容をさっぱり理解していないことがわかったので、改めて整理しています。

参考にした資料は参考文献に列挙しています。中でも主に文献4を参考にしています。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

8章の流れ

統計の目的の一つとして、「未知パラメータの推定」という問題があり、この章ではその中でも「点推定」について扱っています*1。「区間推定」については9章で扱われています。

  • 情報の集約
    • 推論を行うにあたって、生データを全て保存するのではなく、情報を集約できればうれしい（メモリ的に）
    • → 「十分統計量」
  • 推定法
    • パラメータの点推定を行うためにはいくつか方法がある
    • → モーメント法
    • → 最尤推定
  • 推定量の評価、推定量の性質
    • 推定法は複数の方法がある。推定量は、真のパラメータ\theta *2の周辺に集中して欲しい。そこでその期待を満たすかをいくつかの指標で評価する。
    • → 不偏性
      • 推定量に偏り（バイアス）がない推定量が望ましい
      • → クラメール・ラオの不等式 : 不偏推定量の分散の下限を評価
      • → 有効推定量 : クラメール・ラオの不等式を満たす不偏推定量
    • → 漸近的性質
      • 標本サイズを大きくしたと仮定した場合の漸近的な評価基準についての議論
      • → 一致性 : 推定量が真のパラメータ\thetaに確率収束すること
      • → 漸近有効性 : 漸近的な分散が下限に達していること（クラメール・ラオの下限に対応）
      • → 一致性
      • → 漸近正規性

この流れに沿って、確認内容をまとめていこうと思います。

今回は、実際に未知パラメータの推定法として「モーメント法」と「最尤法」について。

【トップに戻る】

パラメータ推定

前提として、データがなんらかのパラメータで規定された確率モデルから生成されているとします。このようなモデルは「パラメトリックなモデル」と呼ばれています。


\begin{align}
 X \sim f(X | \theta_1, \theta_2, \cdots, \theta_k)
\end{align}

モデルとして正規分布を設定すれば、パラメータ\thetaはμとσの二つです。統計的推定では、確率モデルのパラメータ\thetaをデータから推定する問題を扱います*3。

【トップに戻る】

推定法: モーメント法

r次のモーメントとは、確率変数のr乗の期待値です。


\begin{align}
 \mu_r = E[ X^r ]
\end{align}

r次のモーメントをパラメータ\thetaの関数g_r(\theta)として表現します。なお、\theta = (\theta_1, \cdots, \theta_k)です。


\begin{align}
 \mu_r = g_r(\theta)
\end{align}

ここで、r次のモーメントを以下のように近似します。


\begin{align}
 \hat{\mu}_r = \frac{1}{n}\sum X^r_i
\end{align}

これらを合わせるとk個の方程式ができるので、その連立方程式を解くことでパラメータ\thetaの推定値を得るというのがモーメント法ということです。

ベルヌーイ分布のパラメータ推定の例

ベルヌーイ分布\mathrm{Ber}(x | \theta)は、パラメータがイベント発生確率\thetaひとつだけの確率分布です。ベルヌーイ分布に従う確率変数Xの期待値は\thetaなので、結局以下の通りとなります。

f:id:hippy-hikky:20210512120338p:plain

正規分布のパラメータ推定の例

正規分布はパラメータが平均\muと分散[tex:\sigma2]の2つです。

Xの期待値はμですが、E[X^2]は分散V[X]から\mu^2 + \sigma^2となります。

ということで、以下のメモのように分散が標本分散として推定できることがわかりました。

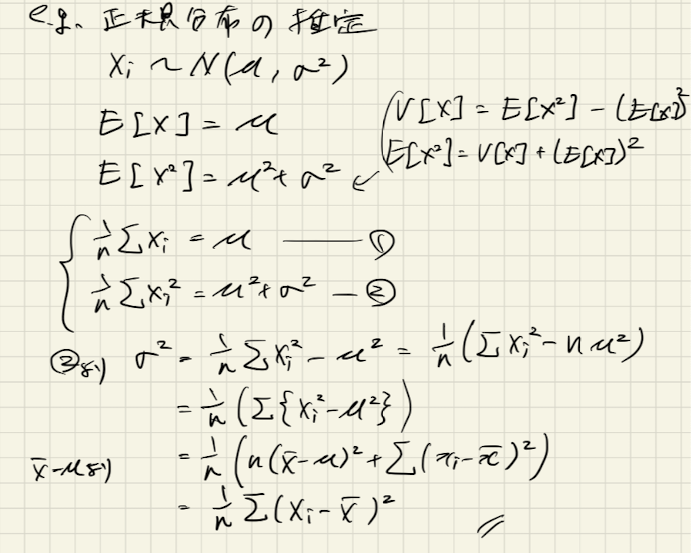
f:id:hippy-hikky:20210512121108p:plain

【トップに戻る】

推定法: 最尤法

サンプルX=(X_1, \cdots, X_n)の同時確率を尤度(likelihood)L(\theta | X)と呼び、尤度が最大になるパラメータθを推定値とするのが最尤法です。

尤度を最大化する意味としては、手元にあるデータが得られる確率が高いパラメータを持ったモデルを選択するのが合理的でしょうという考えに基づいています。このような考えを「最尤原理」と呼ぶと理解しています。

尤度関数を最大化するパラメータを求めるということで、以下のメモのように、パラメータ\theta_iで偏微分して0とした連立方程式を解きます。このとき、尤度関数は総積で表現されるため計算がややこしくなるので、対数をとった対数尤度を使うことが多いです。

f:id:hippy-hikky:20210512122108p:plain

ベルヌーイ分布のパラメータ推定の例

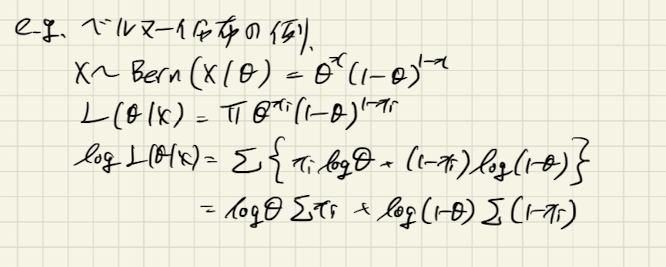
f:id:hippy-hikky:20210512122404p:plain

正規分布のパラメータ推定の例

f:id:hippy-hikky:20210512122418p:plain

【トップに戻る】

参考資料

【トップに戻る】

*1:ここではパラメトリックなモデルを扱っています。ノンパラメトリックな方法については本書に記載があるのかは未確認です。

*2:真のパラメータってなんだ？という議論についてはここでは立ち入らないです。テキストの内容についてなるべく素直に読み解いていきます。

*3:ノンパラメトリックなモデルというのもありますが、ここでは対象外とされています