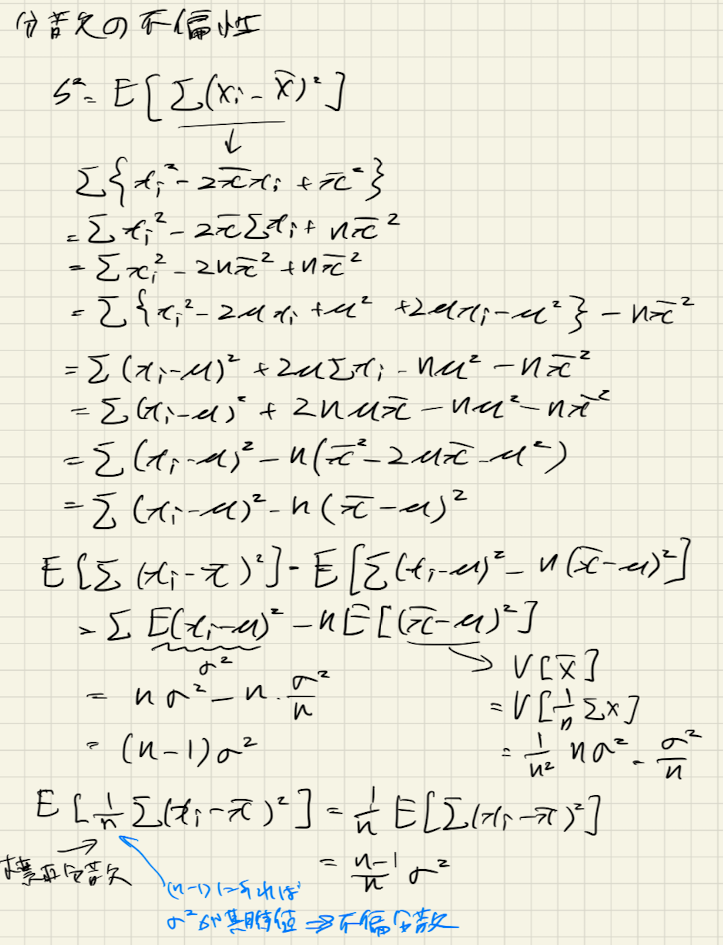【統計検定準一級】第8章 統計的推定の基礎 #4【番外編】
【概要】
- 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズの番外編
- 8章「統計的推定の基礎」の内容をまとめます
- 今回は推定量を評価する基準として、サンプルサイズが大きいときの漸近的な性質を議論します
- 正直理解できてないです。折を見て再度挑戦しよう
- おまけとして、不偏分散の導出も載せています
【目次】
はじめに
「統計学実践ワークブック(参考資料1)」の問題を解いていくシリーズをやっていく中で、8章「統計的推定の基礎」の内容をさっぱり理解していないことがわかったので、改めて整理しています。
参考にした資料は参考文献に列挙しています。中でも主に文献4を参考にしています。
心優しい方、間違いに気付いたら優しく教えてください。
8章の流れ
統計の目的の一つとして、「未知パラメータの推定」という問題があり、この章ではその中でも「点推定」について扱っています*1。「区間推定」については9章で扱われています。
- 情報の集約
- 推論を行うにあたって、生データを全て保存するのではなく、情報を集約できればうれしい（メモリ的に）
- → 「十分統計量」
- 推定法
- パラメータの点推定を行うためにはいくつか方法がある
- → モーメント法
- → 最尤推定
- 推定量の評価、推定量の性質
この流れに沿って、確認内容をまとめていこうと思います。
今回は推定量を評価する基準として、サンプルサイズが大きいときの漸近的な性質を議論します。
推定量の性質
前々回は、パラメトリックなモデルにおけるパラメータの推論方法として、「モーメント法」と「最尤法」を扱いました。
パラメータの推論方法は他にも事後確率最大化法（MAP推定）などの方法がありますが、それらの推定量の性質を評価して、どのような推定量が好ましいのかを議論していきます。
漸近的性質
標本サイズnが大きい時の推定量の性質がわかれば、推定量が良いものか判断できます。
一致性(consistency)
推定量が一致性を持つとは、以下のようにnを大きくしていくと
が真のパラメータ
に確率収束することとあります。
以下の手書きメモにあるように、チェビシェフの不等式を使って導出できることがわかります。
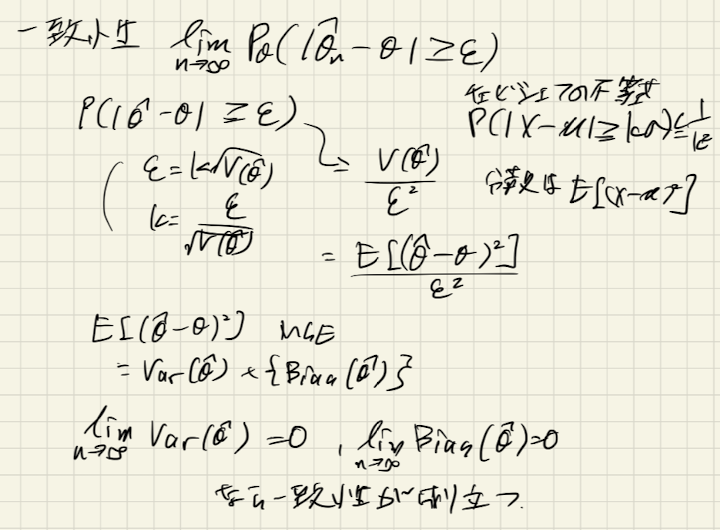
漸近有効性(asymptotic efficiency)
漸近有効性については、用語を整理するだけです（正直理解できてないところです）。
「有効推定量」というのは前回の議論で出てきましたが、分散がクラメール・ラオ下限な不偏分散でした。
「漸近」有効性ということで、漸近的な分散がクラメール・ラオの下限を示すというのが「漸近有効性」です。
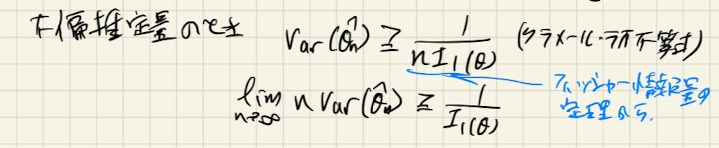
おまけ：分散の不偏性
これだけだと寂しいので、不偏分散の導出をおまけとしてまとめます。
分散といったら標本分散がよく使われていますが(最尤推定量ですし)、前回標本分散にはバイアスがあるということを述べました。そのため、不偏分散と比較していましたが、この不偏分散はなぜあの式なのかを証明してみます。
例によって手書きなので読みにくいと思いますが、やっていることはシンプルです。まず、標本分散の期待値を計算します。この期待値から、真の分散が期待値になるにはどうしたら良いかを考えます。
参考資料
[1] 日本統計学会, 統計学実践ワークブック, 2020, 学術図書出版社
日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック
- 発売日: 2020/05/29
- メディア: 単行本
- 発売日: 1991/07/09
- メディア: 単行本
[3] 矢島ら, 自然科学の統計学, 1992, 東京大学出版会
- 発売日: 1992/08/01
- メディア: 単行本
[4] 久保川, 現代数理統計学の基礎, 2017, 共立出版
- 作者:達也, 久保川
- 発売日: 2017/04/07
- メディア: 単行本
[5] 竹村, 現代数理統計学, 2021, 学術図書出版社
- 作者:彰通, 竹村
- 発売日: 2020/11/10
- メディア: 単行本
