【統計検定準一級】統計学実践ワークブックの問題をゆるゆると解く#24
【概要】
- 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズ
- 第24回は10章「検定の基礎」から1問
【目次】
はじめに
本シリーズでは、いろいろあってリハビリも兼ねて統計学実践ワークブックの問題を解いていきます。 統計検定を受けるかどうかは置いておいて。
今回は10章「検定の基礎」から1問。
なお、問題の全文などは著作権の問題があるかと思って掲載してないです。わかりにくくてすまんですが、自分用なので。
心優しい方、間違いに気付いたら優しく教えてください。
問10.2
問題
あるメーカの既製品Aと新製品Bの重さXは独立に正規分布に従っているとする。それぞれ16個をランダムに抽出して偏差平方和[tex:T2]を算出した。
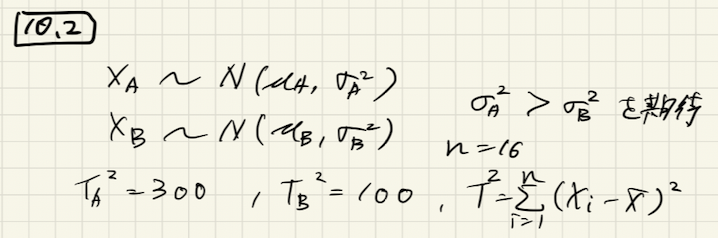
(1) 新製品Bの分散の95%信頼区間を求めよ
偏差平方和を分散で割った値は自由度(n-1)のカイ二乗分布に従います(以下のメモ参照)。

ということで、カイ二乗分布表を使って、95%区間を求めると以下のメモの通りとなります。

(2) 新製品の方が分散が小さいという主張を検定せよ
実際のテキストの問題では穴埋めの問題になっていますが、分散の比について検定してみます。
新製品の方が分散が小さいという主張なので、帰無仮説、対立仮説
は以下の通りとなります。

(1)で扱ったように、偏差二乗和[tex:T2]は自由度(n-1)のカイ二乗分布に従います。
なので、フィッシャーの分散比をH0について求めると、検定統計量はF分布(
)に従うことがわかります。
ということで、検定統計量とF分布表から、帰無仮説は棄却できることがわかります。つまり、新製品の方が分散が小さいという主張が正しそうだと支持されます。


