機械と学習する

統計解析、機械学習について学習したことをまとめていきます

【統計検定準一級】第8章 統計的推定の基礎 #2【番外編】

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズの番外編
  • 8章「統計的推定の基礎」の内容をまとめます
  • 今回は推定法として「最尤法」と「モーメント法」について

【目次】

はじめに

「統計学実践ワークブック(参考資料1)」の問題を解いていくシリーズをやっていく中で、8章「統計的推定の基礎」の内容をさっぱり理解していないことがわかったので、改めて整理しています。

参考にした資料は参考文献に列挙しています。中でも主に文献4を参考にしています。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

8章の流れ

統計の目的の一つとして、「未知パラメータの推定」という問題があり、この章ではその中でも「点推定」について扱っています*1。「区間推定」については9章で扱われています。

  • 情報の集約
    • 推論を行うにあたって、生データを全て保存するのではなく、情報を集約できればうれしい（メモリ的に）
    • → 「十分統計量」
  • 推定法
    • パラメータの点推定を行うためにはいくつか方法がある
    • → モーメント法
    • → 最尤推定
  • 推定量の評価、推定量の性質
    • 推定法は複数の方法がある。推定量は、真のパラメータ\theta *2の周辺に集中して欲しい。そこでその期待を満たすかをいくつかの指標で評価する。
    • → 不偏性
      • 推定量に偏り（バイアス）がない推定量が望ましい
      • → クラメール・ラオの不等式 : 不偏推定量の分散の下限を評価
      • → 有効推定量 : クラメール・ラオの不等式を満たす不偏推定量
    • → 漸近的性質
      • 標本サイズを大きくしたと仮定した場合の漸近的な評価基準についての議論
      • → 一致性 : 推定量が真のパラメータ\thetaに確率収束すること
      • → 漸近有効性 : 漸近的な分散が下限に達していること（クラメール・ラオの下限に対応）
      • → 一致性
      • → 漸近正規性

この流れに沿って、確認内容をまとめていこうと思います。

今回は、実際に未知パラメータの推定法として「モーメント法」と「最尤法」について。

【トップに戻る】

パラメータ推定

前提として、データがなんらかのパラメータで規定された確率モデルから生成されているとします。このようなモデルは「パラメトリックなモデル」と呼ばれています。


\begin{align}
 X \sim f(X | \theta_1, \theta_2, \cdots, \theta_k)
\end{align}

モデルとして正規分布を設定すれば、パラメータ\thetaはμとσの二つです。統計的推定では、確率モデルのパラメータ\thetaをデータから推定する問題を扱います*3。

【トップに戻る】

推定法: モーメント法

r次のモーメントとは、確率変数のr乗の期待値です。


\begin{align}
 \mu_r = E[ X^r ]
\end{align}

r次のモーメントをパラメータ\thetaの関数g_r(\theta)として表現します。なお、\theta = (\theta_1, \cdots, \theta_k)です。


\begin{align}
 \mu_r = g_r(\theta)
\end{align}

ここで、r次のモーメントを以下のように近似します。


\begin{align}
 \hat{\mu}_r = \frac{1}{n}\sum X^r_i
\end{align}

これらを合わせるとk個の方程式ができるので、その連立方程式を解くことでパラメータ\thetaの推定値を得るというのがモーメント法ということです。

ベルヌーイ分布のパラメータ推定の例

ベルヌーイ分布\mathrm{Ber}(x | \theta)は、パラメータがイベント発生確率\thetaひとつだけの確率分布です。ベルヌーイ分布に従う確率変数Xの期待値は\thetaなので、結局以下の通りとなります。

f:id:hippy-hikky:20210512120338p:plain

正規分布のパラメータ推定の例

正規分布はパラメータが平均\muと分散[tex:\sigma2]の2つです。

Xの期待値はμですが、E[X^2]は分散V[X]から\mu^2 + \sigma^2となります。

ということで、以下のメモのように分散が標本分散として推定できることがわかりました。

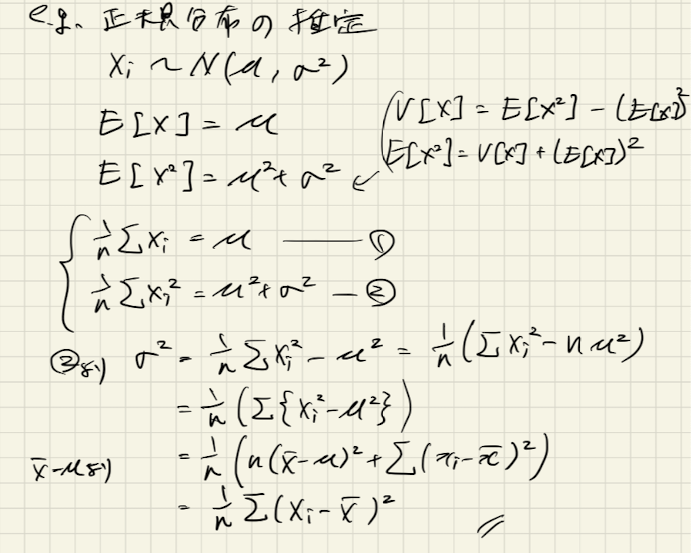
f:id:hippy-hikky:20210512121108p:plain

【トップに戻る】

推定法: 最尤法

サンプルX=(X_1, \cdots, X_n)の同時確率を尤度(likelihood)L(\theta | X)と呼び、尤度が最大になるパラメータθを推定値とするのが最尤法です。

尤度を最大化する意味としては、手元にあるデータが得られる確率が高いパラメータを持ったモデルを選択するのが合理的でしょうという考えに基づいています。このような考えを「最尤原理」と呼ぶと理解しています。

尤度関数を最大化するパラメータを求めるということで、以下のメモのように、パラメータ\theta_iで偏微分して0とした連立方程式を解きます。このとき、尤度関数は総積で表現されるため計算がややこしくなるので、対数をとった対数尤度を使うことが多いです。

f:id:hippy-hikky:20210512122108p:plain

ベルヌーイ分布のパラメータ推定の例

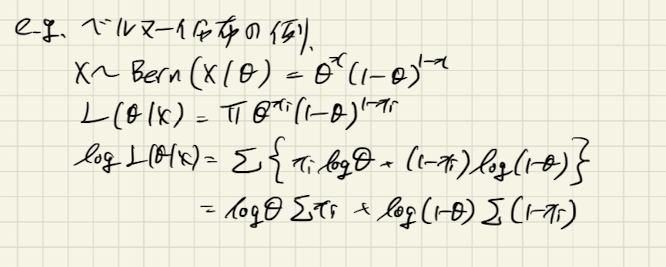
f:id:hippy-hikky:20210512122404p:plain

正規分布のパラメータ推定の例

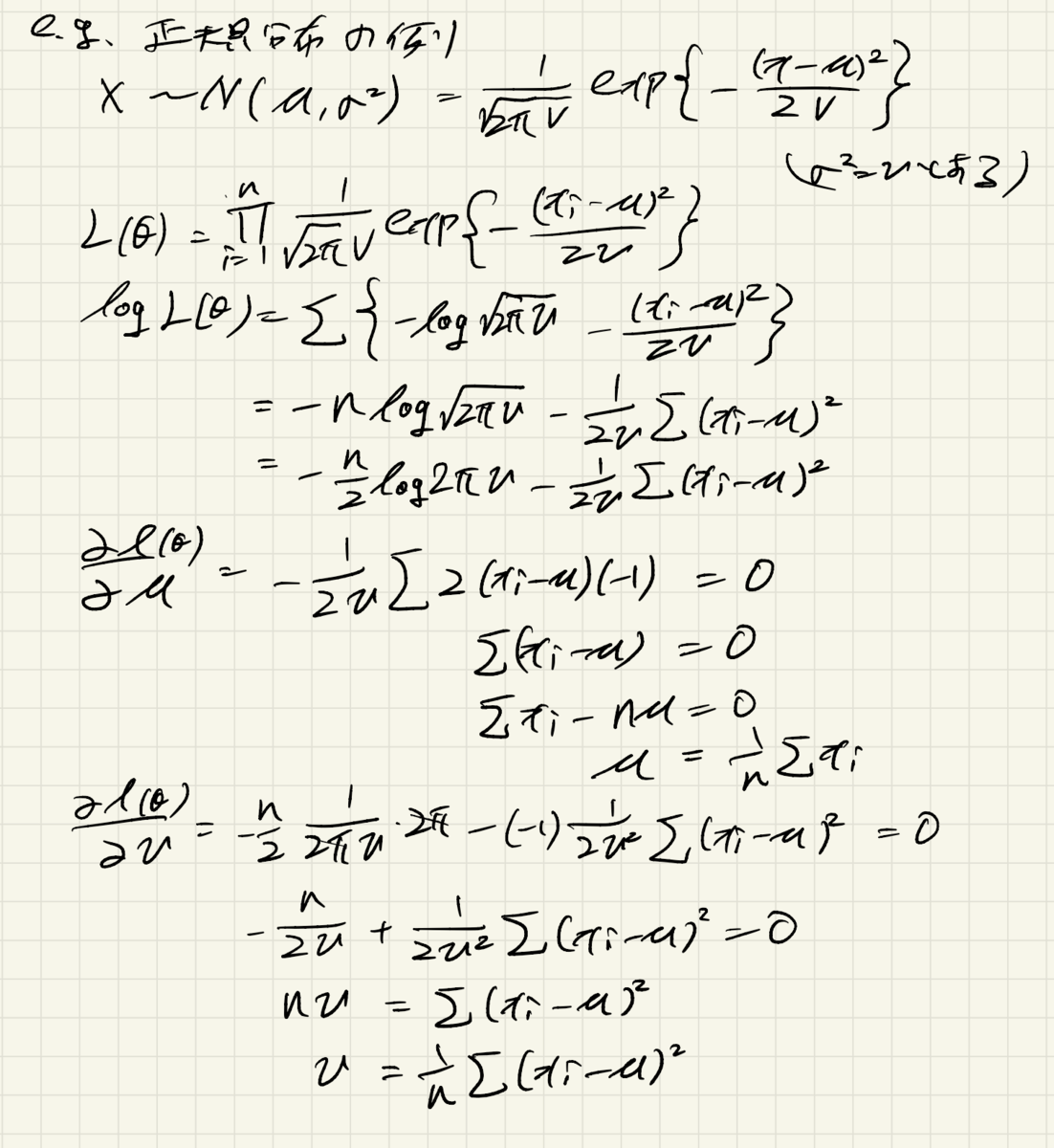
f:id:hippy-hikky:20210512122418p:plain

【トップに戻る】

参考資料

【トップに戻る】

*1:ここではパラメトリックなモデルを扱っています。ノンパラメトリックな方法については本書に記載があるのかは未確認です。

*2:真のパラメータってなんだ？という議論についてはここでは立ち入らないです。テキストの内容についてなるべく素直に読み解いていきます。

*3:ノンパラメトリックなモデルというのもありますが、ここでは対象外とされています

【統計検定準一級】第8章 統計的推定の基礎 #1【番外編】

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズの番外編
  • 8章「統計的推定の基礎」の内容をまとめます
  • 今回は「十分統計量」について

【目次】

はじめに

「統計学実践ワークブック(参考資料1)」の問題を解いていくシリーズをやっていく中で、8章「統計的推定の基礎」の内容をさっぱり理解していないことがわかったので、改めて整理しています。

参考にした資料は参考文献に列挙しています。中でも主に文献4を参考にしています。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

8章の流れ

統計の目的の一つとして、「未知パラメータの推定」という問題があり、この章ではその中でも「点推定」について扱っています*1。「区間推定」については9章で扱われています。

  • 情報の集約
    • 推論を行うにあたって、生データを全て保存するのではなく、情報を集約できればうれしい（メモリ的に）
    • → 「十分統計量」
  • 推定法
    • パラメータの点推定を行うためにはいくつか方法がある
    • → モーメント法
    • → 最尤推定
  • 推定量の評価、推定量の性質
    • 推定法は複数の方法がある。推定量は、真のパラメータ\theta *2の周辺に集中して欲しい。そこでその期待を満たすかをいくつかの指標で評価する。
    • → 不偏性
      • 推定量に偏り（バイアス）がない推定量が望ましい
      • → クラメール・ラオの不等式 : 不偏推定量の分散の下限を評価
      • → 有効推定量 : クラメール・ラオの不等式を満たす不偏推定量
    • → 漸近的性質
      • 標本サイズを大きくしたと仮定した場合の漸近的な評価基準についての議論
      • → 一致性 : 推定量が真のパラメータ\thetaに確率収束すること
      • → 漸近有効性 : 漸近的な分散が下限に達していること（クラメール・ラオの下限に対応）
      • → 一致性
      • → 漸近正規性

この流れに沿って、確認内容をまとめていこうと思います。

今回は、情報の集約としての「十分統計量」について。

【トップに戻る】

情報の集約：十分統計量(sufficient statistics)

上記の通り、生データを全て保持するのではなく、パラメータの推論に必要な情報を抽出して保存しておくことができればうれしいです。しかし、必要な情報が失われては意味がないです。

そこで、パラメータ推論に関する情報を失っていない統計量のことを「十分統計量」と呼んでいるとのことです。パラメータ推論にあたって、「十分統計量」だけを残すようにすれば生データの保持が必要ないということです。

確率変数X、未知のパラメータ\thetaに対して統計量を T(X)=t としたとき、以下の関係が成り立つ T(X) が十分統計量です。


\begin{align}
 P(X=x | T(X)=t, \theta) = P(X=x | T(X)=t)
\end{align}

十分統計量を求めたい

どんな統計量が十分統計量たり得るかということについて、テキストにはi.i.dなデータについて順序統計量は十分統計量か？という例題があります。この例題については、i.i.dであることからデータの順番には意味がないはずです。だから十分統計量になります。

この例題は特殊で、一般にどのような統計量が十分統計量かを求めるために、因子分解定理(fatorization theorem)を使うそうです。

T(X)がXの十分統計量となる必要十分条件


\begin{align}
 f( \mathbf{x} | \theta) = h( \mathbf{x}) g( T(x) | \theta )
\end{align}

と表せる T(x) 。

これの証明は、参考文献4、参考文献5に記載されていました。これらのテキストの証明を順に追って行ったメモをいかに貼り付けておきます。が、連続変数に対しての一般の証明については測度論を使う必要がありめっちゃ難しいということでした（調べてもない。。。）。

f:id:hippy-hikky:20210511165541p:plain

必要条件については分かりやすいのですが、十分条件についての最初の総和の形式に変形するところが理解できてないです。後ほど理解できたら補足しておきます。

十分統計量の導出例: ポアソン分布の場合

確率変数X=\{ X_1, \cdots, X_n\}がポアソン分布\mathrm{Poi}(\lambda)に従って i.i.d でサンプルが得られているとします。ポアソン分布のパラメータ\lambdaを推定するための十分統計量を求める。

f:id:hippy-hikky:20210511165943p:plain

メモの通り、同時確率を\lambdaに依存する項( g(T(X)|\theta) )と依存しない項( h(X) )に分解しました。このg(T(X)|\theta)のうち、Xの統計量として、 \sum X_iが十分統計量となります。

\lambdaを推論するにあたって、\lambdaに依存しない部分は定数となり、最適化にあたっては無視ができるので、h(X)の項は推論に影響を与えないということになると思います。

十分統計量の導出例: 正規分布の場合

（証明はできてないですが）連続変数として正規分布のパラメータを推論するための十分統計量も求めてみます。 簡単のために、分散は1で既知とします。平均パラメータμを推論するための十分統計量を求めるということになります。

f:id:hippy-hikky:20210511170013p:plain

ということで、μを推論するために必要な十分統計量は \bar{X} = \frac{1}{n}\sum X_iであることがわかりました（総和 \sum X_iだけでも良い？）。

ここで、上記メモの2行目から3行目の変換については、以下のようにしてx_iとμを分けています。

f:id:hippy-hikky:20210511170025p:plain

【トップに戻る】

参考資料

【トップに戻る】

*1:ここではパラメトリックなモデルを扱っています。ノンパラメトリックな方法については本書に記載があるのかは未確認です。

*2:真のパラメータってなんだ？という議論についてはここでは立ち入らないです。テキストの内容についてなるべく素直に読み解いていきます。

【統計検定準一級】統計学実践ワークブックの問題をゆるゆると解く#16

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズ
  • 第16回は8章「統計的推定の基礎」から1問
  • きびしい

【目次】

はじめに

本シリーズでは、いろいろあってリハビリも兼ねて統計学実践ワークブックの問題を解いていきます。 統計検定を受けるかどうかは置いておいて。

今回は8章「統計的推定の基礎」から1問。8章はいきなり厳しくて、参考書を2冊追加してます（会社の経費で買った）。

なお、問題の全文などは著作権の問題があるかと思って掲載してないです。わかりにくくてすまんですが、自分用なので。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

問8.1

問題

正規分布\mathcal{N}(\mu, \sigma^2)からi.i.dで得た標本X=\{X_1, \cdots, X_n \}について

(1) \sum(X_1 - \mu)^2は統計量か？

「統計量」の定義は、「標本のみの関数」となるため、これは統計量ではない。

(2) 順序統計量を並べたベクトルはパラメータ\mu, \sigma^2の十分統計量か？

「順序統計量」は標本を並べ替えただけのものです。Xはi.i.dなので、並べ替えても尤度は同じになります。そのため、元のXと順序統計量はパラメータの推定に関して情報が失われてはいないため、これは「十分統計量」と言えます。

f:id:hippy-hikky:20210508233046p:plain

(3) 標本分散\frac{1}{n}\sum (X_i - \bar{X})^2は不偏推定量か？

分散の不偏推定量はnで割るのではなく、(n-1)で割る必要があるので、これは不偏推定量ではありません。

不偏分散自体は記憶していたのですが、不偏分散の証明が追えていないので後で確認しておきます。。。

(4) 標本分散の平方根は標準偏差の最尤推定量か？

正規分布の最尤推定量を導出すると、以下のメモの通りとなります。

この結果から、標本分散が分散の最尤推定量ということがわかります。

f:id:hippy-hikky:20210508233540p:plain

(5) 標本分散は分散\sigma^2の一致推定量であるが、漸近有効推定量ではないか？

これはわかりません。後で確認します。漸近論が全く理解できていない。

【トップに戻る】

参考資料

【トップに戻る】

【統計検定準一級】統計学実践ワークブックの問題をゆるゆると解く#15

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズ
  • 第15回は7章「極限定理、漸近理論」から2問
  • 7章、例題は解けたけど、ぶっちゃけ理解している自信がない

【目次】

はじめに

本シリーズでは、いろいろあってリハビリも兼ねて統計学実践ワークブックの問題を解いていきます。 統計検定を受けるかどうかは置いておいて。

今回は7章「極限定理、漸近理論」から2問。

なお、問題の全文などは著作権の問題があるかと思って掲載してないです。わかりにくくてすまんですが、自分用なので。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

問7.1

問題

普通のサイコロを30回投げる。このとき、数字の3が十回以上現れる確率はいくつになるか？

回答

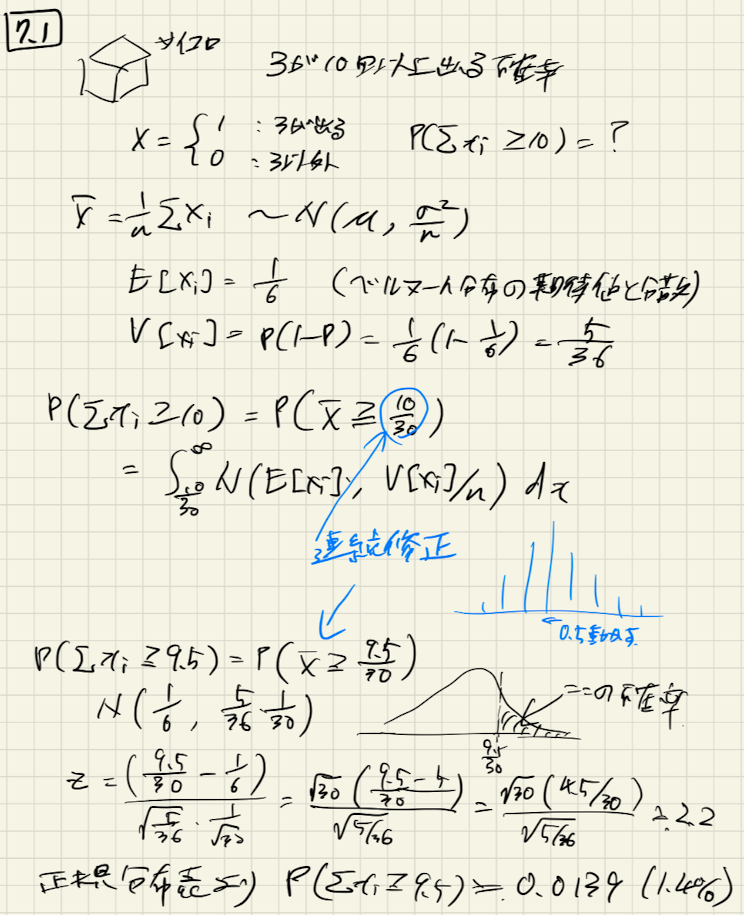
3が出ると出ないの2分類で考えると、各試行はベルヌーイ試行になります。そのため、各試行の期待値と分散がわかります。

次に、3が10回以上ということなので、確率変数の和、または、平均は中心極限定理から正規分布に従います。

ということで、確率変数の平均\bar{X}が\bar{X} \ge \frac{10}{30}となる確率を求めれば良いことがわかります。正規分布なので、標準正規分布に変換して、標準正規分布表を使って確率を求められます。

ここで、「連続修正」をしろと問いに記載があります。連続修正については正直よくわかっていませんが、離散変数の区間を半分(0.5)ずらすということなんですかね？？私が持っている参考書には記載がなさそうだったので。。。（よく探したら書いてあるのかもですが）

f:id:hippy-hikky:20210507164820p:plain

問7.2

問題設定

\left\{X_n \right\}は独立同分布に従う確率変数。\bar{X_n}は標本平均。

f:id:hippy-hikky:20210507170616p:plain

(1) \frac{\sqrt{n}(\bar{X}_n - \mu)}{\sigma}が収束する分布

7.1で出てきた中心極限定理から、標準正規分布に収束することがわかります。

f:id:hippy-hikky:20210507170831p:plain

(2) \frac{\sqrt{n}(\bar{X}^3_n - \mu^3)}{\sigma}が収束する分布

テキストに書かれている「デルタ法」を使うことでどのような分布に収束するかがわかります。

これはテキストに例が書かれていてその例とほぼ一緒です。

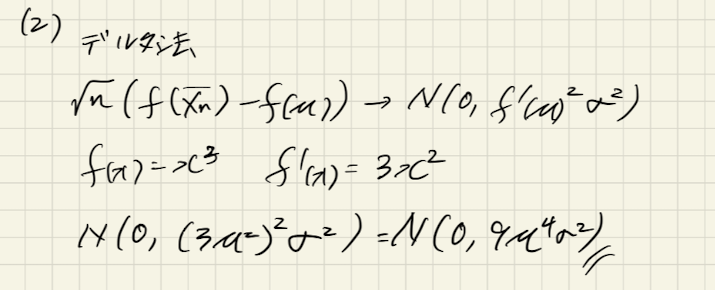
f:id:hippy-hikky:20210507171019p:plain

(3) \left(\frac{\sqrt{n}(\bar{X}_n - \mu)}{\sigma} \right)^2が収束する分布

カッコの中身は(1)の通り標準正規分布に収束します。標準正規分布に従う変数（以下ではZとおく）の二乗が収束する分布ということで、カイ二乗分布に収束します。

f:id:hippy-hikky:20210507171233p:plain

【トップに戻る】

参考資料

【トップに戻る】

【統計検定準一級】統計学実践ワークブックの問題をゆるゆると解く#14

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズ
  • 第13回は6章「連続型分布と標本分布」から1問
  • 6章長かった

【目次】

はじめに

本シリーズでは、いろいろあってリハビリも兼ねて統計学実践ワークブックの問題を解いていきます。 統計検定を受けるかどうかは置いておいて。

今回は6章「連続型分布と標本分布」から1問。

なお、問題の全文などは著作権の問題があるかと思って掲載してないです。わかりにくくてすまんですが、自分用なので。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

問6.4

問題設定

統計学の試験を計500人（文系が300人、理系が200人）が受けた。試験の得点は、文系、理系の受験者に対応する2つのコンポーネントを持つ混合正規分布で表現できるとする。

f:id:hippy-hikky:20210506181259p:plain

(1) AさんとBさんの偏差値を求めよ

Aさんは文系で67点、Bさんは理系で82点だった。

ということで、偏差値の定義（平均50、標準偏差10）に合わせてスコアを変換します。

f:id:hippy-hikky:20210506181628p:plain

(2) 60点以上を合格とした場合、この試験全体での合格率はおよそいくらか？

コンポーネントが二つの混合正規分布で表現されるということなので、確率密度関数f(x)は以下の手書きメモの通りです。混合比は人数比です。

60点以上の確率を導出すれば良いので、f(x)を60から∞まで積分します。正規分布の積分を頑張って計算するのは大変なので、標準正規分布に変換しておおよその値を求めます。

f:id:hippy-hikky:20210506181706p:plain

【トップに戻る】

参考資料

【トップに戻る】

【統計検定準一級】統計学実践ワークブックの問題をゆるゆると解く#13

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズ
  • 第13回は6章「連続型分布と標本分布」から1問

【目次】

はじめに

本シリーズでは、いろいろあってリハビリも兼ねて統計学実践ワークブックの問題を解いていきます。 統計検定を受けるかどうかは置いておいて。

今回は6章「連続型分布と標本分布」から1問。

なお、問題の全文などは著作権の問題があるかと思って掲載してないです。わかりにくくてすまんですが、自分用なので。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

問6.3

問題設定

生存関数としてパラメータ\lambdaを持つ指数分布を仮定。

f:id:hippy-hikky:20210505210327p:plain

(1) 確率密度関数を求めよ

確率密度関数の定義は積分して1となることです。確率変数Tの性質上、負の範囲はとらないので、0から∞までの積分結果を正規化定数とすれば良いです。

f:id:hippy-hikky:20210505210945p:plain

(2) 確率密度関数の平均と上側25%点を求めよ

平均を導出するにあたって、期待値の定義通りに計算する方法とモーメント母関数を利用する方法があります。私は後者のモーメント母関数を利用しました。

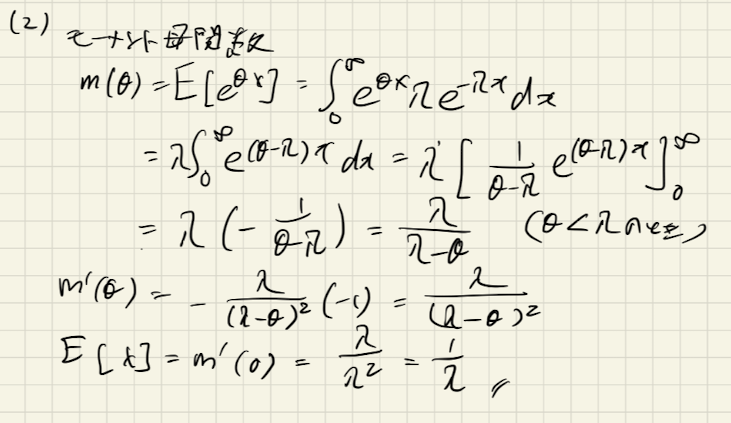
f:id:hippy-hikky:20210505211246p:plain

次に、上側25%点ですが、累積分布関数が0.75となる位置となります。

そこでまず初めに累積分布関数F(x)を導出します。その後に0.75を代入して結果を得ます。

f:id:hippy-hikky:20210505211258p:plain

(3) 平均生存時間が3年だったとして、上側25%点の推定値を求めよ

平均生存時間が3年ということで、このモデルのパラメータ\lambdaの推定値を単純な最尤推定量として導出します。このパラメータの推定量を(2)で導出した結果に代入します。

f:id:hippy-hikky:20210505211640p:plain

【トップに戻る】

参考資料

【トップに戻る】

【統計検定準一級】統計学実践ワークブックの問題をゆるゆると解く#12

統計検定準一級

【概要】

  • 統計検定準一級対応 統計学実践ワークブックの問題を解いていくシリーズ
  • 第12回は6章「連続型分布と標本分布」から1問

【目次】

はじめに

本シリーズでは、いろいろあってリハビリも兼ねて統計学実践ワークブックの問題を解いていきます。 統計検定を受けるかどうかは置いておいて。

今回は6章「連続型分布と標本分布」から1問。

なお、問題の全文などは著作権の問題があるかと思って掲載してないです。わかりにくくてすまんですが、自分用なので。

心優しい方、間違いに気付いたら優しく教えてください。

【トップに戻る】

問6.2

問題設定

英語の試験において、Listening、Reading、Totalの平均と標準偏差は以下のメモの通りであった。

f:id:hippy-hikky:20210504220430p:plain

(1) ListeningとReadingの点数の間の相関係数を求めよ

相関係数は、共分散を標準偏差で割ったものになります。また共分散は、確率変数の和の分散の性質から導出できます。

ということで、値を代入することで容易に導出できます。

f:id:hippy-hikky:20210504220647p:plain

(2) ListeningとReadingの点数が2変量正規分布に従うとしたとき、Listeningの点数が335点の人らのReadingの条件付き期待値はいくらか？

点数が多変量正規分布に従うということで、多変量正規分布の条件付き分布を求めれば良いです。

テキストに条件付き分布の平均ベクトルと分散共分散行列が書かれているので値を代入することで解が導けます。

f:id:hippy-hikky:20210504221201p:plain

[補足]多変量ガウス分布の条件付き分布

ここで、多変量ガウス分布の条件付き分布についてですが、以前「ガウス過程と機械学習」の輪読会の際に証明を導出していたので、そのメモを貼り付けておきます。

条件付き分布の証明については、参考文献に貼っているとおり、ガウス過程と機械学習やPRMLなどに証明の過程が多少書かれていますのでそちらを参考にされたら良いと思います。私が所有している版では「ガウス過程と機械学習」には誤植が散見されるのでPRMLの方が良いかもしれません。

f:id:hippy-hikky:20210504221521p:plain

つづきます

f:id:hippy-hikky:20210504221537p:plain

ということで、テキストの通りになることがわかります。

【トップに戻る】

参考資料

【トップに戻る】